Abstract

在编码孔径快照光谱压缩成像(CASSI)系统中，采用高光谱图像重建(HSI)方法从 compressed measurement 数据中恢复空间光谱信号。

在这些算法中，deep unfolding 方法表现出良好的性能，但存在两个问题。

首先，它们没有从高度相关的CASSI 中估计退化模式和病态程度来指导迭代学习。

其次，它们主要使用基于 CNN 的方法，在捕获长程依赖时表现出局限性。

这篇文章提出了一个 principled Degradation-Aware Unfolding 框架(DAUF)，从 compressed image 和 physical mask 估计参数，然后使用这些参数来控制每次迭代。

此外，这篇文章还定制了一种新的 Half-Shuffle Transformer (HST)，它可以同时捕获 local contents 和 non-local dependencies。

通过将 HST 插入到 DAUF 中，建立了第一种基于 Transformer 的 deep unfolding 方法—— Degradation-Aware Unfolding Half-Shuffle Transformer (DAUHST)，用于HSI重构。

Introduction

高光谱图像比普通RGB图像具有更多的光谱波段，可以存储更详细的信息。因此，HSI 被广泛应用于图像识别、目标检测、跟踪、医学图像处理、遥感等领域。为了获得 HSI ，传统的成像系统使用光谱仪沿着光谱或空间维度扫描场景，通常需要很长时间。这些成像系统无法捕捉动态物体。最近，快照压缩成像(SCI)系统已被开发用于以视频速率捕获HSI。在这些SCI系统中，编码孔径快照光谱成像(CASSI)以其令人印象深刻的性能脱颖而出。CASSI 使用编码孔径和 disperser 在不同波长调制 HSI 信号，然后混合所有调制信号产生二维压缩 measurement。随后，采用 HSI 复原方法解决CASSI逆问题，即从 measurement 恢复 HSI。这些方法分为 4 类:

基于模型的方法依赖于手工制作的图像先验，如 total variation，sparsity，low-rank等。这些方法有理论推到证明并且具有可解释性。此外，这些方法需要手工调整参数，这减慢了重构速度。同时，它们的表征能力和泛化能力也很有限。
即插即用(plug -and-play, PnP)算法将预训练的去噪网络插入传统的基于模型的方法，以解决HSI重构问题。然而，PnP方法中预训练的网络是固定的，不再训练，因此限制了性能。
端到端(E2E)算法使用一个强大的模型，通常是卷积神经网络(CNN)，来学习从measurement 到期望的 HSI 的端到端映射函数。端到端方法具有深度学习的能力。然而，他们从压缩 measurement 到底层光谱图像学到的是一种暴力映射，从而忽略了CASSI系统的工作原理。它们没有经过理论验证的特性、可解释性和灵活性，因为不同硬件系统的成像模型之间存在很大差异。
Deep unfolding 方法采用多级网络将 measurement 结果映射到 HSI 立方体中。每一阶段通常包括两个阶段，即先通过线性投影，然后将信号通过学习底层降噪先验的单阶段网络。在 deep unfolding 方法中，通过显式地刻画图像先验和系统成像模型，可以直观地解释网络结构。此外，这些方法还具有深度学习的力量，具有很大的潜力。然而，这一潜力尚未得到充分探索。

现有的深度展开算法存在两个问题:

迭代学习与CASSI系统高度相关。然而，目前的展开方法并没有在每次迭代中估计 CASSI 退化模式和病态度来调整线性投影和去噪网络。
现有的深度展开方法主要基于CNN，因此在捕捉非局部自相似性和远程依赖性方面存在局限性，而这两者对 HSI 重建至关重要。

由于 Transformer 建模非局部空间区域交互的强大能力，其被广泛用于图像分类、目标检测、语义分割、人体姿态估计，图像复原等。但使用 Transformer 面临两个问题： 1) 全局 Transformer 对空间维度的计算复杂度是二次方倍。 2) 基于窗口的 Transformer 感受野有限。

针对上述问题，这篇文章首先提出了基于最大后验概率(MAP)理论的 principled Degradation-Aware Unfolding Framework(DAUF) 用于 HSI 重建。

与以前的 deep unfolding 方法不同，DAUF 从 degraded compressed measurement 和 physical mask 隐式估计信息参数。

然后，DAUF将获取 CASSI degradation patterns 和 ill-posedness degree 关键线索的参数输入到每次迭代中，自适应缩放线性投影，并为去噪网络提供噪声水平信息。

其次，设计了一种新的 Half-Shuffle Transformer (HST)作为每次迭代的去噪先验。HST可以联合提取局部上下文信息和建模非局部依赖关系，同时需要比全局 Transformer 更便宜的计算成本。

通过定制一种 Half-shuffle Multi-head Self-Attention (HS-MSA)机制来实现这一点，该机制构成了HST的基本单元。

具体来说，HS-MSA有两个分支，即 local 分支和 non-local 分支。local 分支在窗口内计算自注意力，而 non-local 分支 shuffle tokens 并且捕获跨窗口的交互。将 HST 插入到 DAUF 中，建立了一个迭代结构，即 Degradation-Aware Unfolding Half-Shuffle Transformer (DAUHST)。

使用提出的技术，DAUHST模型大大超过了最先进的(SOTA)深度展开方法，在相同的阶段数超过4 dB。

简而言之，这篇文章的贡献概括如下：

制定了一个 principled MAP-based unfolding framework DAUF 用于HSI重建
提出了一种新型的 Transformer HST，并将其插入到 DAUF 中建立 DAUHST。DAUHST 可能是第一个基于 transformer 的HSI重建 deep unfolding 方法
在需要更少的计算和内存成本的同时，DAUHST在很大程度上优于SOTA方法。此外，在真实的HSI重建中，DAUHST的视觉效果更好。

Proposed Method

Degradation-Aware Unfolding Framework

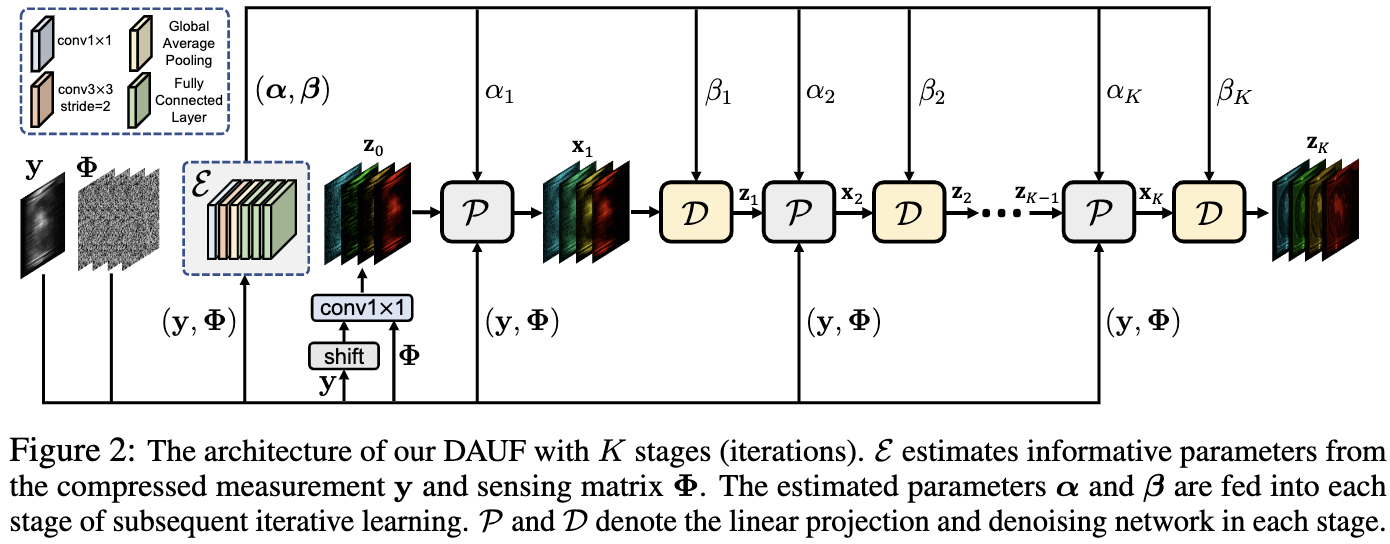
以前的展开框架[43,44,45,46]没有估计 CASSI 退化模式来调整迭代学习。为了缓解这一限制，这篇文章制定了一个principled Degradation-Aware Unfolding Framework(DAUF)，如图2所示。DAUF 来自 MAP 理论。原始HSI信号可以通过最小化以下能量函数来估计：

$\hat x = \mathop{\text{argmin}}_x \frac{1}{2} \| y - \Phi x \|^2 + \tau R(x) \tag{2}$ 其中 $\frac{1}{2}|y - \Phi x|^2$ 是数据保真项， $R(x)$ 是图像先验项，并且 $\tau$ 是超参数调节重要性。通过引入辅助变量 $z$, 等式 $2$ 可以公式化为：

\[\hat x = \mathop{\text{argmin}}_x \frac{1}{2} \| y - \Phi x \|^2 + \tau R(z) \qquad s.t. \quad z = x \tag{3}\]

这是一个约束优化问题。为了得到展开推理，采用 half-quadratic splitting (HQS) 算法以简化和快速收敛。等式 $3$ 可以通过最小化下列等式求解：

$L_\mu(x, z) = \frac{1}{2}\|y - \Phi x\|^2 + \tau R(z) + \frac{\mu}{2} \|z - x\|^2 \tag{4}$ 其中 $\mu$ 是惩罚项，其强制 $x$ 和 $z$ 接近。等式 $4$ 可以通过将 $x$ 和 $z$ 分解为下面两个迭代子问题求解：

\[x_{k+1} = \mathop{\text{argmin}}_x \| y - \Phi x\|^2 + \mu \|x - z_k \|^2 \\ z_{k+1} = \mathop{\text{argmin}}_z \frac{\mu}{2} \| z - x_{k+1}\|^2 + \tau R(z) \tag{5}\]

其中 $k = 0, 1, …, K -1$ 表示迭代次数。数据保真项和一个二次正则化最小二乘问题相关，如等式 $5$ 中的 $x_{k+1}$。它的 closed-form 解为：

\[x_{k + 1} = (\Phi^T\Phi + \mu I)^{-1}(\Phi^Ty + \mu z_k) \tag{6}\]

其中 $I$ 是对角矩阵。因为 $\Phi$ 是 fat 矩阵， $\Phi^T\Phi + \mu I$ 会很大，因此通过矩阵求逆公式简化$(\Phi^T \Phi + \mu I)^T$求逆问题的计算：

\[(\Phi^T\Phi + \mu I)^{-1} = \mu^{-1} I - \mu^{-1} \Phi^T (I + \Phi \mu^{-1} \Phi^T)^{-1}\Phi \mu^{-1} \tag{7}\]

通过将等式 $7$ 插入等式 $6$，我们可以重公式化等式 $6$

\[x_{k+1} = \frac{\Phi^\top y + \mu z_k}{\mu} - \frac{\Phi^\top(I + \Phi \mu^{-1}\Phi^\top)^{-1} \Phi \Phi^\top y}{\mu^2} - \frac{\Phi^\top (I + \Phi \mu^{-1} \Phi^\top)^{-1}\Phi z_k}{\mu} \tag{8}\]

在 CASSI 系统中， $\Phi \Phi^\top$ 是对角矩阵，其可以定义为 $\Phi \Phi^\top \stackrel{def}= \text{diag}{\phi_1, …, \phi_n}$。通过插入 $\Phi \Phi^\top$ 到 $(I + \Phi \mu^{-1} \Phi^\top)^{-1}$ 和 $(I + \Phi \mu^{-1} \Phi^\top)^{-1} \Phi \Phi^\top$, 得到：

\[(I + \Phi \mu^{-1} \Phi^\top)^{-1} = \text{diag} \left\{\frac{\mu}{\mu + \psi_1}, ..., \frac{\mu}{\mu + \psi_n}\right\} \\ (I + \Phi \mu^{-1} \Phi^\top)^{-1}\phi \phi^\top = \text{diag} \left\{\frac{\mu \psi_1}{\mu + \psi_1}, ..., \frac{\mu \psi_n}{\mu + \psi_n}\right\} \tag{9}\]

令 $y \stackrel{def} = [y_1, …, y_n]^\top$ 和 $[\Phi z_k]_i$ 表示 $\Phi z_k$ 的第 $i$ 个元素。将 $9$ 插入 $8$ 有：

\[\begin{align} x_{k + 1} &= \frac{\Phi^\top y}{\mu} + z_k - \frac{1}{\mu} \Phi^\top \left[ \frac{y_1\psi_1 + \mu[\Phi z_k]_1}{\mu + \psi_1}, ..., \frac{y_n\psi_n + \mu[\Phi z_k]_n}{\mu + \psi_n}\right] \\ &= z_k + \Phi^\top \left[\frac{y_1 - [\Phi z_k]_1}{\mu + \psi_1}, ..., \frac{y_n - [\Phi z_k]_n}{\mu + \psi_n} \right]^\top \end{align} \tag{10}\]

注意到 ${y_i - [\Phi z_k]i}{i=1}^n$ 可以直接通过 $y - \Phi z_k$ 更新，并且 ${\phi_i}_{i=1}^n$ 被预先计算出来存储在 $\Phi \Phi^\top$。因此，等式 $10$ 中的 element-wise 的计算可以被非常有效地更新。根据等式 $5$，惩罚参数 $\mu$ 应该足够大，以便 $x$ 和 $z$ 接近相同的固定点。这表示 $\mu$ 控制每次迭代的收敛和输出。因此，相比于手动调整 $\mu$, 将 $\mu$ 设置为 iteration-specific 的参数，其从 CASSI 系统中自动估计。我们将第 $k$ 次迭代的 $\mu$ 表示为 $\mu_k$ 。

回到等式 $5$，作者也设置 $\tau$ 为 iteration-specific 的参数， $z_{k+1}$ 可以被重公式化为：

$z_{k+1} = \mathop{\text{argmin}}_z \frac{1}{2(\sqrt{\tau_{k+1} / \mu_{k+1}})^2} \| z - x_{k+1} \|^2 + R(z) \tag{11}$ 从贝叶斯概率的角度，等式 $11$ 等价于高斯噪声在 level $\sqrt{\tau_{k+1}/\mu_{k+1}}$ 时，对图像 $x_{k+1}$ 去噪。为了方便求解等式 $11$, 设置 $\frac{1}{(\sqrt{\tau_{k+1} /\mu_{k+1}})^2} = \mu_{k+1} / \tau_{k+1} $ 作为从CASSI系统估计的参数。令 $\alpha_k \stackrel{def}= \mu_k$, $\alpha \stackrel{def}=[\alpha_1, …, \alpha_K]$， $\beta_k \stackrel{def}= \mu_k / \tau_k$ $\beta \stackrel{def}= [\beta_1, …, \beta_K]$。然后可以重公式化 DAUF 为一个迭代：

\[(\alpha, \beta) = \xi(y, \Phi) ，\quad x_{k+1} = \mathcal{P}(y, z_k, \alpha_{k+1}, \Phi), \quad z_{k+1} = \mathcal{D}(x_{k+1}, \beta_{k+1}) \tag{12}\]

其中 $\xi$ 表示从CASSI 系统的压缩 measurement $y$ 和 sensing matrix $\Phi$ 中的参数估计器， $\mathcal{P}$ 等价于等式 $10$ 表示的线性投影， $\mathcal{D}$ 表示高斯去噪器求解等式 $11$。 $z_0$ 被通过 shift 的 $y$ 和 $\Phi$ 拼接通过 $conv1 \times 1$ 初始化。图 2 展示了 $\xi$ 的结构。它包含一个 $conv1 \times 1$，一个 strided $conv3 \times 3$，一个全局平均池化和三个全连接层。通过 $\xi$, DAUF 通过学习由 mask-modulation 和 dispersion-integration 导致的退化模式和病态度从 CASSI 系统中捕获关键线索。参数 $\alpha$ 和 $\beta$ 从 $\xi$ 估计，通过自适应缩放等式 $10$ 中的线性投影指导迭代学习，并且为等式 $11$ 中去噪器先验提供噪声等级信息。

Experiment

Quantitative Comparisons with State-of-the-Art Methods

表一展示了不同方法的 FLOPs, PSNR 和 SSIM。

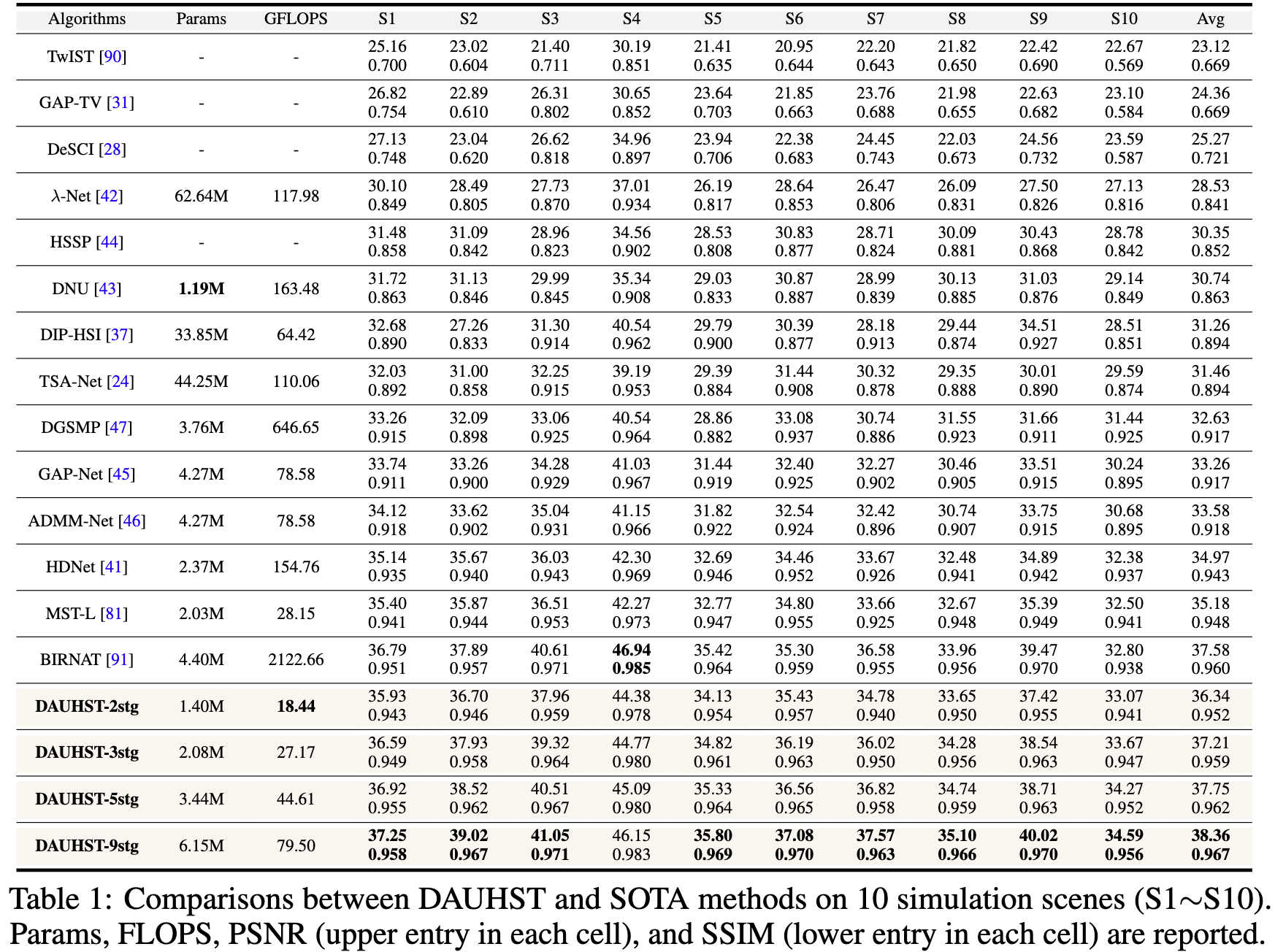
（i）最好的模型DAUHST-9stg(9 stage DAUHST)产生了非常令人印象深刻的结果，即PSNR为38.36 dB, SSIM为0.967。DAUHST-9stg 明显优于最近的两种SOTA方法 BIRNAT 和 MST-L，分别为0.78和3.18 dB，表明该方法的有效性。

（ii） DAUHST 模型大大超过了SOTA方法，同时需要更便宜的计算和内存成本。DAUHST-2stg 超出 MST-L 1.16 dB 并且仅需要 68.9% (1.40/2.03)的参数以及 65.5%(18.44/28.15) 的 FLOPs。与基于 CNN 的端到端方法相比，DAUHST-3stg比HDNet、TSA-Net和-Net高出2.24、5.75和8.68 dB，而只需要87.8%、4.7%、3.3%的参数和17.6%、24.7%、23.0%的FLOPS。与基于 RNN 的端到端方法BIRNAT相比，DAUHST-5stg高0.17 dB，但只花费2.1%的FLOPS和78.2%的Params。与基于CNN的深度展开方法相比，DAUHST-3stg的性能比ADMM-Net(9 stage)和GAP-Net(9 stage)分别高出3.63和3.95 dB，但仅花费48.7% Params和34.6% FLOPS。图1 绘制了 DAUHST 和SOTA展开方法的PSNR-FLOPS比较。在相同的 stage 数下，DAUHST的性能超过了其他竞争对手 4dB。

Qualitative Comparisons with State-of-the-Art Methods

Simulation HSI Reconstruction. 图4是 DAUHST 方法和其他SOTA方法在场景2上用4个光谱通道(共28个)进行模拟HSI重建的对比。右上部分显示了整个 HSI 中被放大的黄色框块。可以看出，DAUHST-9stg更有利于重建视觉愉悦的 HSI, 有详细的内容，更干净的纹理，和更少的 artifacts，同时保持均匀区域的空间平滑。相比之下，以前的方法要么产生过度光滑的结果，损害细粒度结构，要么引入在真实(GT)图像中没有的 chromatic artifacts 和 blotchy textures。中上部分显示了密度-波长光谱曲线，对应于RGB图像中标识为a和b的绿色方框(左上)。该算法的光谱曲线与参考曲线的相关性和一致性最高，显示了该算法在光谱维一致性重建方面的优势。

Real HSI Reconstruction. 作者进一步评估了DAUHST在真实HSI重建中的有效性。为了进行公平的比较，按照与[24,47,81]相同的设置，在CAVE和KAIST数据集上用真实 mask重新训练 DAUHST-3stg。模拟真实的成像情况，训练样本也注入了 11-bit shot 噪声。图5展示了 DAUHST-3stg 与9种SOTA方法的视觉对比。在前三行中，只有DAUHST-3stg能够重构出所有波长下黄色方框所对应的花朵patch，而其他方法都无法恢复整个patch。在最下面一行中，DAUHST-3stg还原了更多的HSI结构细节，内容更清晰， artifacts 更少。相比之下，其他方法恢复图像模糊，产生不完整的响应，并容易受到噪声的破坏。这一证据表明，DAUHST对噪声失真有更强的鲁棒性，在真实HSI重建中更有效。

Conclusion

这篇文章弥补了以往 deep unfolding 方法存在的两个问题:

1)它们不估计来自CASSI系统的信息参数来指导迭代学习

2) 它们主要基于CNN，在捕获远程依赖性方面显示出局限性。

为了解决这些挑战，首先制定了基于 principled MAP-based unfolding framework DAUF，从compressed measurement 和physical mask 估计参数。

然后，将获取 CASSI degradation patterns 和 ill-posedness degree 的关键线索的参数用于每次迭代，以 contextually scale 线性投影，并为去噪网络提供噪声水平信息。

其次，这篇文章提出了一种新的Transformer HST，它可以联合提取局部内容和建模非局部依赖。

通过将 HST 插入 DAUF，得到首个基于 Transformer 的 unfolding 方法 DAUHST 用于 HSI 重构。

【深度学习】DAUHST: Degradation-Aware Unfolding Half-Shuffle Transformer for Spectral Compressive Imaging