Abstract

快照压缩成像(SCI)系统已被开发用于使用低维 off-the-shelf 传感器捕捉高维(>=3)信号，即将多个视频帧映射到单个 measurement 帧。

SCI系统的一个关键模块是一个准确的解码器，可以恢复原始视频帧。

然而，现有的基于模型的解码算法需要利用先验知识进行彻底的参数调优，由于运行时间过长，无法支持实际应用。

这篇文章提出了一种用于视频SCI系统的 Deep Tensor ADMM-Net，它可以在秒内提供高质量的解码。

首先，从一个标准的 tensor ADMM 算法开始，将其推理迭代展开到一个 layer-wise 结构中，并设计了一个基于张量运算的深度神经网络。

其次，网络不依赖于预先指定的稀疏表示域，而是通过随机梯度下降法学习低秩张量域。

值得注意的是，提出的 Deep Tensor ADMM-Net 具有潜在的数学解释。

在公共视频数据上的仿真结果表明，该方法的PSNR平均提高0.8 2.5 dB, SSIM平均提高0.07 0.1，提速1500-3600次。

在SCI相机捕获的真实数据上，实验结果显示了与最先进的方法相比较的视觉效果，但运行时间更短

Video SCI Systems and Tensor Model

Snapshot Compressing Imaging System

在 video SCI 系统 (例如, CACTI) 如图1所述，考虑 $B$ 帧视频 $\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times B}$ 是由 $B$ 个 sensing matrices(mask) $\mathcal{C} \in \mathbb{R}^{n_1 \times n_2 \times B}$调制和压缩的， measurement 帧 $Y \in \mathbb{R}^{n_1 \times n_2}$ 可以表述为：

\[Y = \sum_{b=1}^B \mathcal{C}^{(b)} \odot \mathcal{X}^{(b)} + N \tag{1}\]

数学上, (1) 中的 measurement 可以用下面的线性等式表达：

$y = \Phi x + n \tag{2}$ 其中 $y = Vec(Y) \in \mathbb{R}^{n_1n_2}$ 并且 $n = Vec(N) \in \mathbb{R}^{n_1n_2}$。相应地，视频信号 $x \in \mathbb{R}^{n_1n_2B}$ 是：

$x = Vec(\mathcal{X}) = [Vec(\mathcal{X}^{(1)})^T, ..., Vec(\mathcal{X}^{(B)})^T]^T \tag{3}$ 与传统的压缩感知不同， video SCI 中的 sensing matrix 是稀疏的并且呈现出对角块结构：

\[\Phi = [\text{diag}(Vec(\mathcal{C}^{(1)})), ..., \text{diag}(Vec(\mathcal{C}^{(B)})) ] \tag{4}\]

因此，采样率这里等于 $1 / B$。

因为 video 是沿着时间的帧序列，将 video 表示为 3D/4D 数组(张量) 并且将 video SCI 解码任务视为从随机线性 measurements 重构一个三阶张量是很直观的。

Tensor Operations

为了重构张量 $\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times B}$, SCI 解码器基于定义1中的 Tesnor Nuclear-Norm 定义。一个 3D 张量 $\mathcal{X}$ 通常可以被视为一个在三维空间中由 $n_1 \times n_2$ 的二维矩阵组成的。将张量 $\tilde{\mathcal{X}}$ 表示为 $\mathcal{X}$ 在频域表示，在每个 tube 上通过傅里叶变换得到，如 $\tilde X(i, j, :) = fft(\mathcal{X}(i, j, :))$ 。

Definition 1. Tensor Nuclear-Norm (TNN) 张量 $\mathcal{T}$ 的 tensor nuclear norm 被定义为 $|T|{TNN} = |\bar T|$, 其中 $|·|_$ 表示 matrix nuclear norm, 例如所有 frontal slices 的奇异值的和 $\tilde{\mathcal{T}^{(b)}}, b \in {1, …, B}$ ，并且 $\bar{\mathcal{T}}$ 表示三阶张量 $\tilde{\mathcal{T}}$ 的对角块形式：

\[\bar{\mathcal{T}} \stackrel{\triangle}= \begin{matrix} \left[\begin{array}{rr} \tilde{\mathcal{T^{(1)}}} & & & \\ & \tilde{\mathcal{T^{(2)}}} & & \\ & & \cdots & \\ & & & \tilde{\mathcal{T^{(B)}}} \end{array}\right] \end{matrix} \in \mathbb{C}^{n_1 B \times n_2B} \tag{5}\]

TNN 已经被证明在 tensor multi-rank 的 $l_1$范数的情况下是 tightest convex relaxation。通过泛化傅里叶变换到其他满秩时间-频率域变换，将 $|\mathcal{T}|{\Lambda, TNN} = |\bar{\mathcal{T}}|{\Lambda, *}$ 表示为在变换 $\Lambda$ 下 $\mathcal{T}$ 的 TNN。

Problem Formulation

这项工作将视频SCI系统中的重建任务建模为一个张量恢复问题，并使用多个变换域下的TNN最小化作为约束。值得注意的是，作者不像[18]那样将低秩性强加于非局部相似patch组，而是将低秩性强加于整个视频(张量)，但在不同的变换域[17]上。为此，将视频SCI重构问题归结为多个变换域的加权凸优化问题

\[\mathop{\text{argmin}}_{\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times B}} \sum_{f=1}^F w_f \| \mathcal{X} \|_{\Lambda_f, TNN} \quad s.t. \quad y = \Phi x + n \tag{6}\]

其中 $w_f$ 表示与变换 $\Lambda_f$ 相关的权重。总共有 $F$ 种变换。采用变换矩阵的通用形式, $(6)$ 中的优化问题等价于：

\[\mathop{\text{argmin}}_{\mathcal{X} \in \mathbb{R}^{n_1 \times n_2 \times B}} \sum_{f=1}^F w_f \| \bar{\mathcal{X}_f} \|_{\Lambda_f, *} + \mathbb{1}_{y = \Phi x + n} \tag{7}\]

其中 $\Lambda = [\Lambda_1, …, \Lambda_F]$ 表示变换矩阵，$\bar{\mathcal{X}}$ 由 $\tilde{\mathcal{X}_f}$ 构造， $\tilde{\mathcal{X}_f}$ 由 $\mathcal{X}$ 构造， $1$ 表示 indicator function.

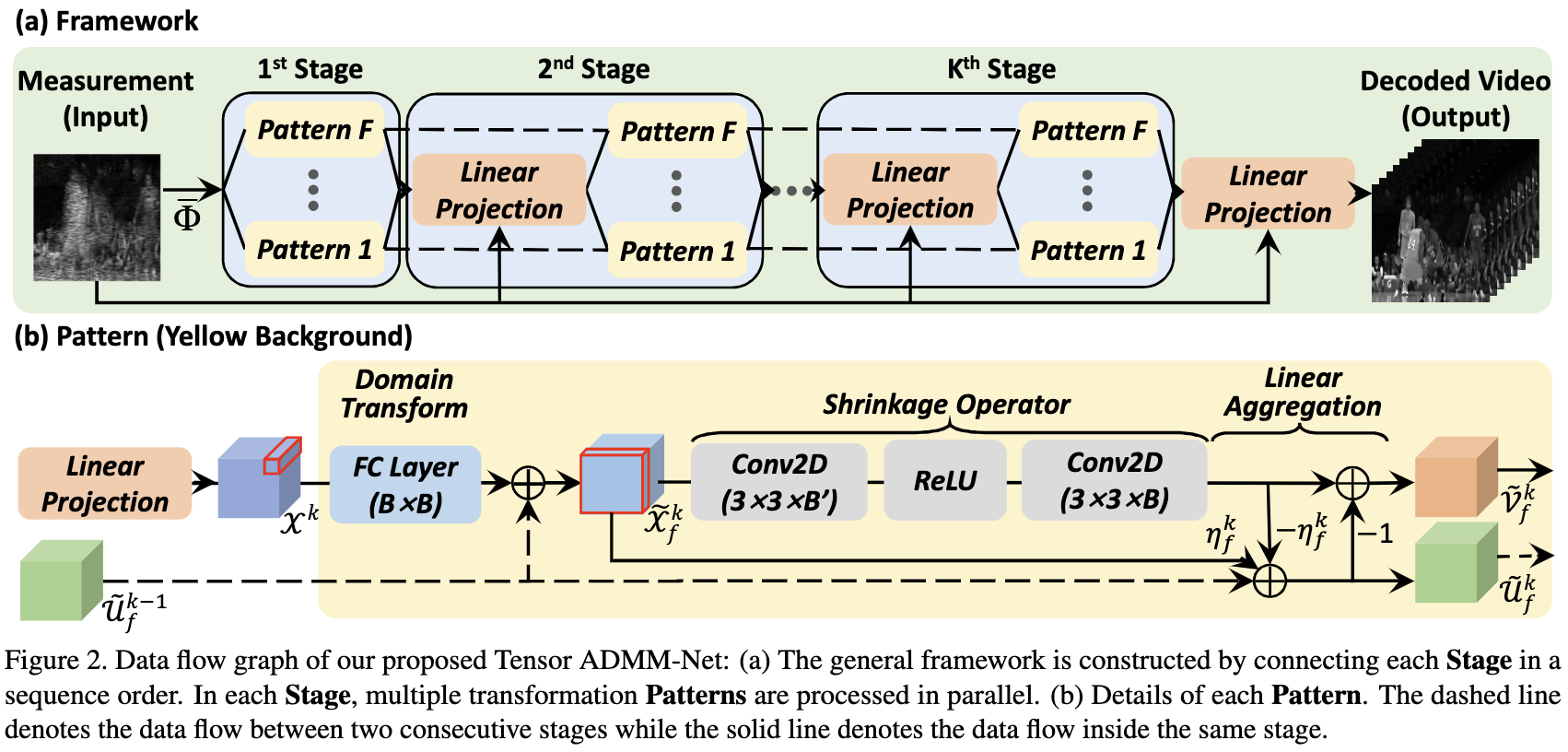
对于 video SCI 解码，我们可以从问题 $(7)$ 得到迭代算法，并且运行大量的迭代之后得到一个满意的重构。然而，设置超参数，如变换矩阵 $\Lambda_f$ 和相关权重 $w_f$，是很有挑战性的并且调整对不同的场景调整这些参数也并不简单。为了发掘神经网络的学习能力，如图2所示，这篇文章开发了一个在每次迭代(stage)中基于 layer-wise 结构的机制。不依赖预先指定的稀疏表示领域知识，而是跨层解耦模型参数，以获得一种新的网络结构，并使用随机梯度下降法训练模型。通过这种方式，变换和权重可以以微分的方式学习。

Deep Tensor ADMM-Net

TNN-ADMM Algorithm

通过使用 ADMM 框架并且引入辅助变量 $\tilde{\mathcal{Z}} = [\tilde{\mathcal{Z_1}, …, \tilde{\mathcal{Z}_f}}]$， $(7)$ 可以写作：

$\mathop{\text{argmin}}_{\mathcal{X}, \tilde{\mathcal{Z}}} \frac{1}{2} \| y - \Phi x\|_2^2 + \sum_{f=1}^F w_f \|\bar{\mathcal{Z}_f}\|_{\Lambda_f, *} \quad s.t. \quad \tilde{X_f} = \tilde{Z_f} \tag{8}$ 与 $\mathcal{X}$ 类似， $\bar{\mathcal{Z}}$ 由 $\tilde{\mathcal{Z}}$ 得到。其可以通过下列子问题求解：

\[\mathcal{X}^k = \mathop{\text{argmin}}_{\mathcal{X}} \left\{\sum_{f=1}^F\left<\tilde{\mathcal{U}_f^{k-1}, \tilde{\mathcal{X}_f - \tilde{\mathcal{Z}_f}}}\right> + \frac{1}{2}\|y-\Phi x\|_F^2 + \sum_{f=1}^F \frac{\rho_f}{2}\| \tilde{\mathcal{X}_f} - \tilde{\mathcal{Z}_f^{k-1}} \|_F^2\right\} \tag{9}\]

$\tilde{\mathcal{Z}_f^k} = \mathop{\text{argmin}}_{\tilde{\mathcal{Z}_f}}\{\left<\tilde{\mathcal{U}_f^{k-1}, \tilde{\mathcal{X}_f^k - \tilde{\mathcal{Z}_f}}}\right> + w_f\|\bar{\mathcal{Z_f}}\|_* + \frac{\rho_f}{2}\|\tilde{\mathcal{X}_f - \tilde{\mathcal{Z}_f}\|_F^2}\} \tag{10}$ $\tilde{\mathcal{U}_f}^k = \tilde{\mathcal{U}_f}^{k-1} + \eta_f(\tilde{X_f^k - \tilde{Z_f^k}}) \tag{11}$

其中 $\tilde{\mathcal{U}} = [\tilde{U_1}, …, \tilde{U_f}]$ 和 $\rho = [\rho_1, …, \rho_F]$ 表示 ADMM 框架中的 multipliers 和拉格朗日展开的 coefficients， $\eta_f$ 是一个决定步长的常数。由于变换矩阵是独立的，对不同的变换域更新 $(10)$ 和 $(11)$ 在相同的迭代中中可以并行和独立地处理。如前所述，这种基于优化的算法虽然可能会得到很好的结果，但由于计算工作量大，需要花费很长时间。在接下来的文章中，使用一个深度网络来解决这个问题，称为 Deep Tensor ADMM-Net。

Pipeline Design for Tensor ADMM-Net

从等式 $(9)$ 到等式 $(11)$ 得到，图2展示了 stage-wise 深度模型结构。在每个 stage，我们首先聚集之前 stage 由 Linear Projection 模块得到的输出，然后将输出送入另一个并行 Patterns 进一步处理。

Linaer Projection

通过采用来自等式 $(9)$ 的等式， Linear Projection 模块聚集 measurement 和前一阶段所有 patterns 的输出，目标是重构想要的信号：

$\mathcal{X}^k = S^k(\Phi^\top y + \sum_{f=1}^F \rho_f^{k+1} \prod_f^k(\tilde{\mathcal{Z}}_f^{k-1} - \tilde{\mathcal{U}}_f^{k-1})) \\ S^k = (\Phi^\top \Phi + \sum_{f=1}^F \rho_f^k \Pi_f^k \Pi_f^{k\top})^{-1} \\ \Pi_f^k = \Lambda_f^k \otimes I_{n_1n_2} \tag{12}$ 其中 $I_{n_1n_2} \in \mathbb{R}^{n_1n_2 \times n_1n_2}$ 表示单位矩阵， $\otimes$ 表示 Kronecker(tensor) product 并且 $\Lambda^k = [\Lambda_1^k, …, \Lambda_F^k]$ 是在第 $k$ 个阶段通用的变换矩阵，其和参数 $\rho^k = [\rho_1^k, …, \rho_F^k]$ 在模型训练期间学习。通过设置 $\tilde{\mathcal{Z}}^0$ 和 $\tilde{\mathcal{U}}^0$ 为零矩阵，我们定义：

$\bar \Phi = S^1 \Phi^\top \tag{13}$ 其将被用于初始化网络的输入(图2(a)所示的输入)。然而 $S^{k+1} \in \mathbb{R}^{n_1 n_2 B \times n_1n_2B}$ 在每个 stage 将会占用大量的内存，使得梯度计算时不可行。受到 $(4)$ 中对角块结构的启发，以及基于 tensor 的与变换，作者进一步调研了内部结构并且减少了处理复杂度。

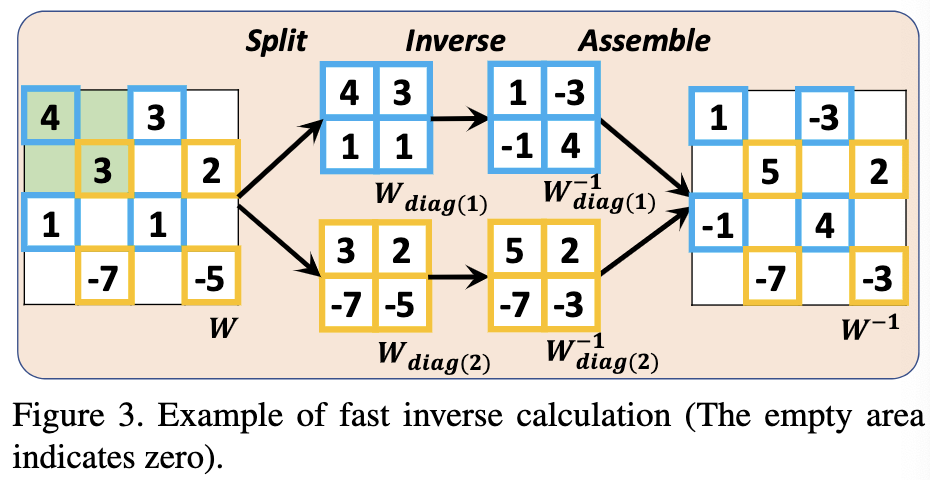
Rectangular Diagonal Block(RDB) 结构是 $n$-by-$n$ 对称对角矩阵的 $B \times B$ 的矩阵，其在 plane 上形成一个 $nB \times nB$ 的矩形矩阵。由 RDB 结构的矩阵应该是满秩的、可逆的、以及每个对称对角矩阵是一个 block。如图3所示，对于有 RDB 结构的矩阵 $W$，绿色背景表示一个 block。相较于直接计算 $W^{-1}$，逆矩阵通过下列步骤计算：

Pattern

采用等式 $(10)-(11)$，作者设计了每个 pattern 的内部结构以实现辅助变量的更新。根据等式 $(10)$， $\tilde{\mathcal{Z}_f^k}$ 的更新包含 nuclear-norm 最小化以及最小平方项。因此，作者首先引入定义 2 中相关理论的的 matrix shrinkage operator，然后求解。

Definition 2. Singular value shrinkage operator. 给定 rank-r 矩阵 $X = U \Sigma V^\top$ 的 SVD 和 $\Sigma = \text{diag}({\sigma_i}_{1 \leq i \leq r})$ ，对于每个 $\tau \geq 0$， soft-thresholding operator 定义为一个 singular value shrinkage operator:

$\mathcal{D}_\tau(X) = U\mathcal{D}_\tau(\Sigma) V^\top \tag{14}$ $D_\tau(\Sigma) = \text{diag}({\max(\sigma_i - \tau, 0)}_{i \leq i \leq r}) \tag{15}$ Theorem 1. 对于每个 $\tau \geq 0$ 并且 $M \in \mathbb{R}^{n_1 \times n_2}$，定义2中的 singular value shrinkage operator 满足：

\[D_\tau (M) = \mathop{\text{argmin}}_X\{\frac{1}{2}\|X - M\|_F^2 + \tau\|X\|_*\} \tag{16}\]

Soft-thresholding 在 $l_1-norm$ 最小化中用于 singular value shrinkage operator，并且这个理论表明这样的一个在辅助矩阵 $M$ 上的操作等价于最小化最小平方和 $l_1-norm$ 的组合。 $(10)$ 的解可以被描述为 $\tilde{\mathcal{Z}^k} = \mathcal{D}_{1 / \rho} (\tilde{U}^{k-1} + \tilde{\mathcal{X}^k})$。由于 TNN 被定义为所有 frontal slices 的奇异值的和， shrinkage operator 可以单独用于每个 frontal slice。

Domain Transformer: 如图2(b)所示，全连接(FC)层在每个 pattern 开始作为 domain transformer。每个 tube $\mathcal{X}_f^k(i, j, :) \in \mathbb{R}^{1 \times B}$ 以并行的方式单独被送入 FC 层。

Shrinkage Operator: [12] 表明 multi-layer feed forward networks(FFN) 对于任意的 vector-valued 函数是 unversal approximates。此外，shrinkage operator 本质上是一个非线性函数，在 video 的每一项中都采用了它，它可以用 vector-value 的形式来描述。由于这个操作在图像上使用，因此，使用 2D 卷积层在 frontal slices, 其中除了最后一层外，每一层的 kernels 数量 $B’ > B$，例如作者将三维像素作为每个空间单元对应的特征向量。

Linear Aggregation: pattern 的 linear aggregation 来自等式 $(11)$ 中 multiplier $\tilde{\mathcal{U}_f^k}$。常数 $\eta_f$ 视为可训练变量，因此对于不同 stages 的不同 pattern 的步长可变。为了便于 4.2.1 解的计算，直接计算 $\tilde{\mathcal{V}}_f^k = \tilde{\mathcal{Z}_f^k} - \tilde{\mathcal{U}}_f^k$ 作为 pattern 的输出。

Conclusion

这篇文章为快照压缩成像系统提出了一种 Deep Tensor ADMM-Net，可以在秒内提供高质量的解码。

将低秩张量模型嵌入到 ADMM 框架中，并将迭代展开到神经网络阶段，因此网络具有潜在的数学解释。

在仿真和真实的 SCI 相机数据上的实验表明，提出的方法展示了优越的性能，并优于目前最先进的算法。

【深度学习】Deep Tensor ADMM-Net：Deep Tensor ADMM-Net for Snapshot Compressive Imaging