YOLO V1
Overview
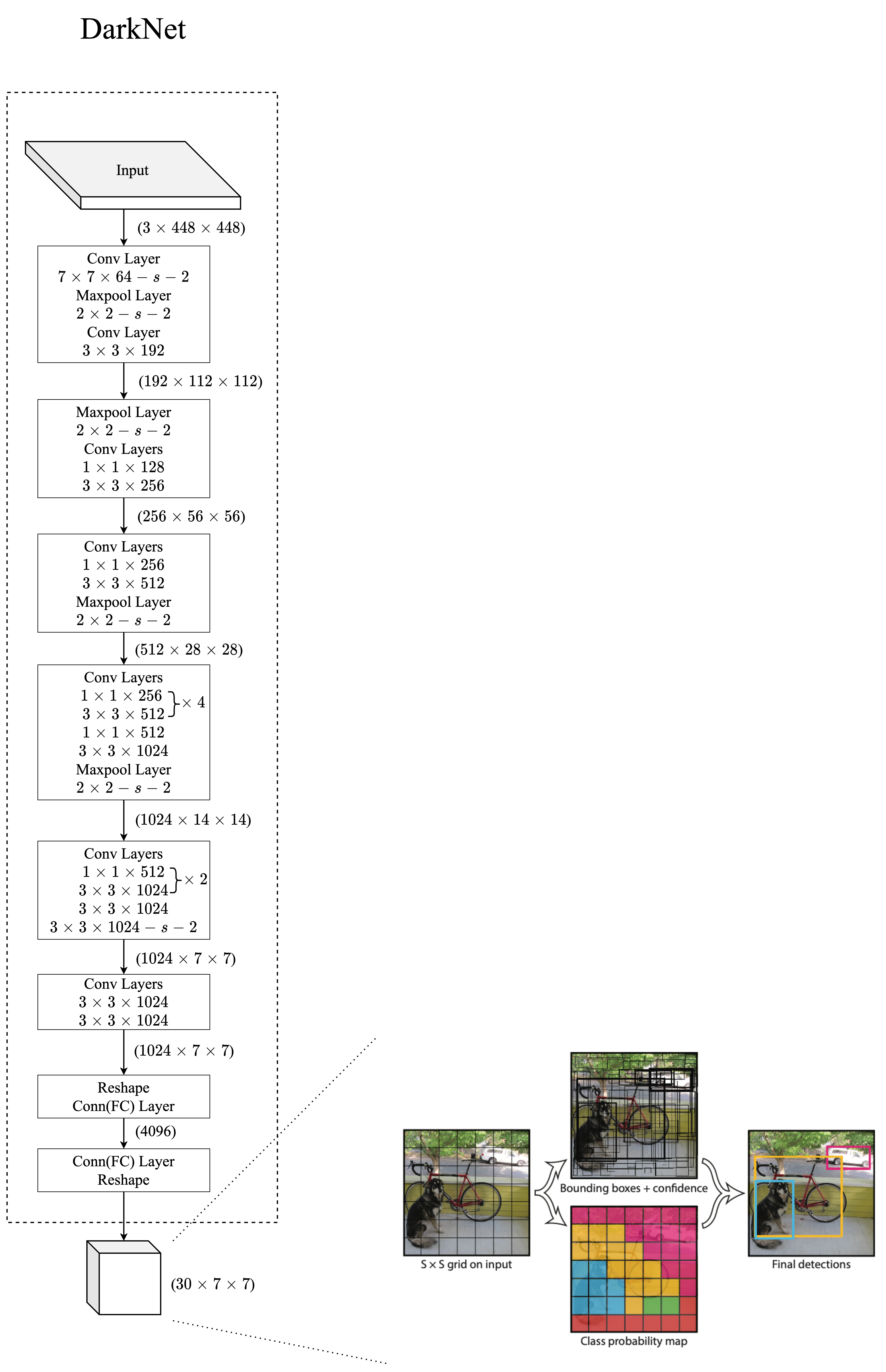
Darknet
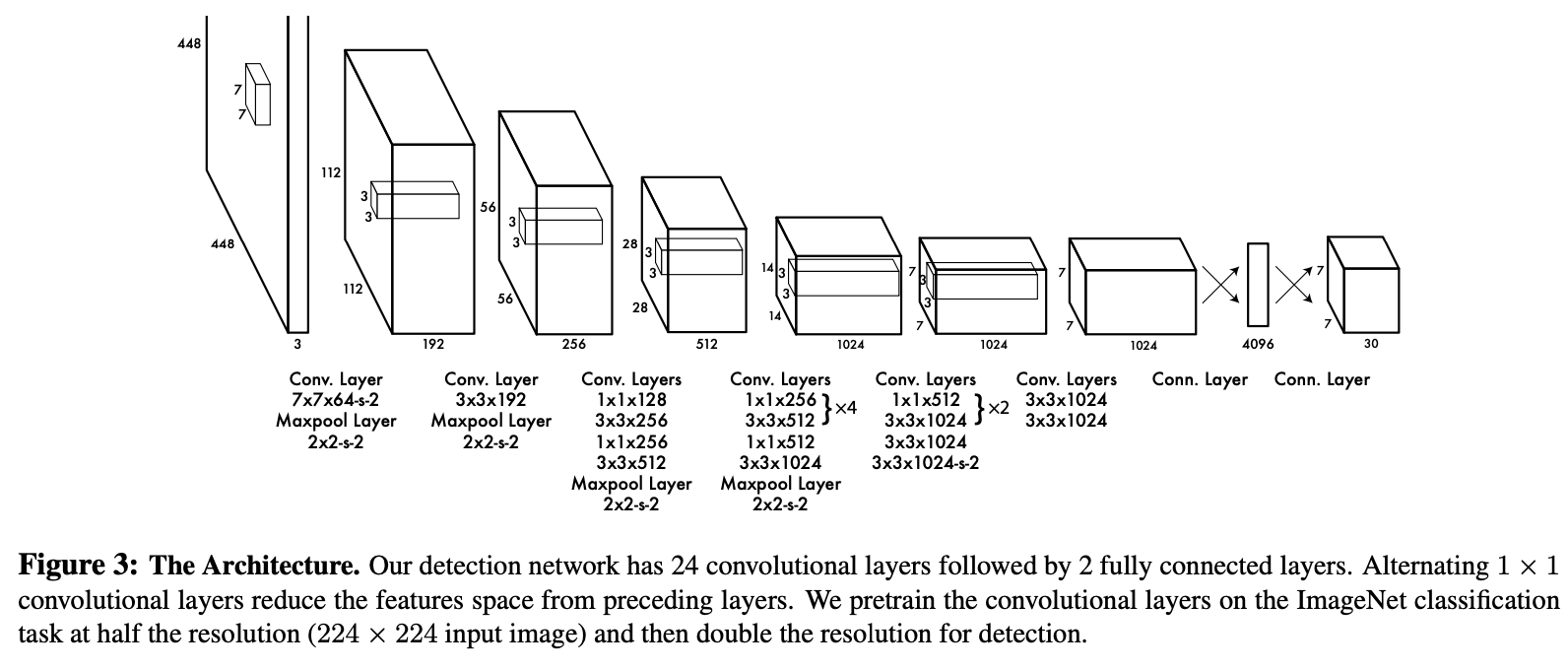
作者使用1×1 reduction layers,然后使用 3×3 卷积层
Loss 计算
$$ l = \lambda_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb{1}_{ij}^{obj} [(x_i - \hat x_i)^2 + (y_i - \hat y_i)^2] \
- \lambda_{coord} \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb{1}_{ij}^{obj}[(\sqrt{w_i} - \sqrt{\hat w_i})^2 + (\sqrt{h_i} - \sqrt{\hat h_i})^2] \
- \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb{1}_{ij}^{obj}(C_i - \hat C_i)^2 \
- \lambda_{noobj} \sum_{i=0}^{S^2} \sum_{j=0}^B \mathbb{1}{ij}^{noobj} (C_i - \hat C_i)^2 \ + \sum{i=0}^{S^2} \mathbb{1}i^{obj} \sum{c \in \text{classes}}(p_i(c) - \hat p_i(c))^2
$$
binary_cross_entropy_with_logits
sigmoid_focal_loss
\[Out = -Labels * alpha * (1 - \sigma(Logit))^{gamma} \log(\sigma(Logit)) - (1 - labels) * (1 - alpha) * \sigma(Logit)^{gamma} \log(1 - \sigma(Logit))\]训练
推理
YOLO V2
YOLO V3
YOLO V4
YOLO V5
YOLO X
#
-
Previous
【深度学习】Segmentation Transformer(OCRNet): Object-Contextual Representations for Semantic Segmentation -
Next
【深度学习】YOLO9000(YOLO V2): Better, Faster, Stronger