条件概率公式与高斯分布的KL散度

条件概率的一般形式

\[P(A, B, C) = P(C \mid B, A) P(B, A) = P(C \mid B, A) P(B \mid A) P(A)\] \[P(B, C \mid A) = P(B \mid A) P(C \mid A, B)\]

基于马尔科夫假设的条件概率

如果满足马尔科夫链关系 $A \rightarrow B \rightarrow C$，那么有：

$P(A, B, C) = P(C \mid B, A) P(B, A) = P(C \mid B) P(B \mid A) P(A)$ $P(B, C \mid A) = P(B \mid A) P(C \mid B)$

高斯分布的 KL 散度公式

对于两个单一变量的高斯分布 $p$ 和 $q$ 而言，它们的 KL 散度为：

\[KL(p, q) = \log \frac{\sigma_2}{\sigma_1} + \frac{\sigma^2 + (\mu_1 - \mu_2)^2}{2 \sigma_2^2} - \frac{1}{2}\]

重参数技巧

若希望从高斯分布 $N(\mu, \sigma)$ 中采样，可以先从标准发布 $N(0, 1)$ 采样出 $z$，再得到 $\sigma * z + \mu$。这样做的好处是将随机性转移到变量 $z$ 上，而 $\sigma$ 和 $\mu$ 当做仿射变换网络的一部分。

VAE 与多层 VAE

单层 VAE 的原理公式与变分下界

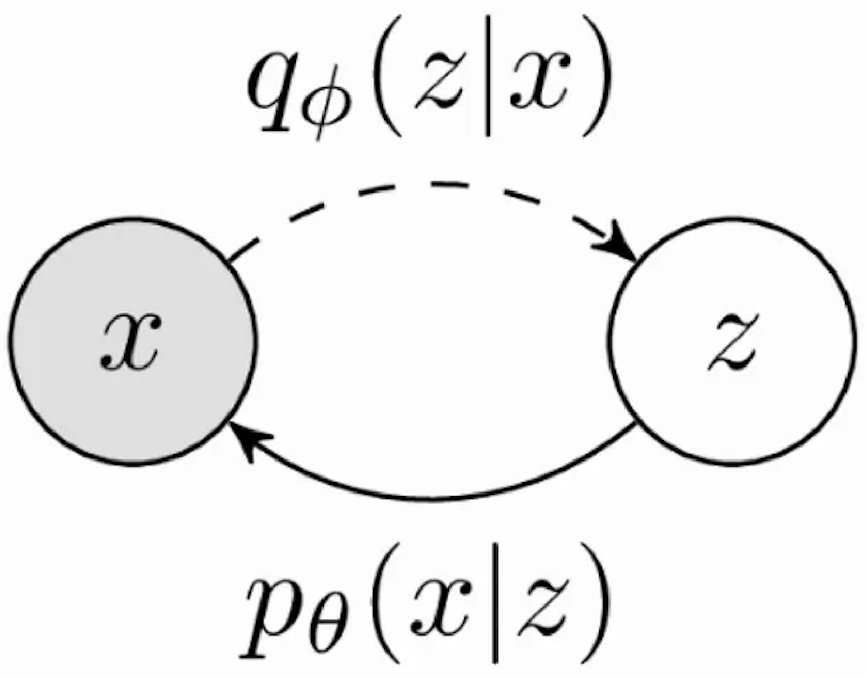
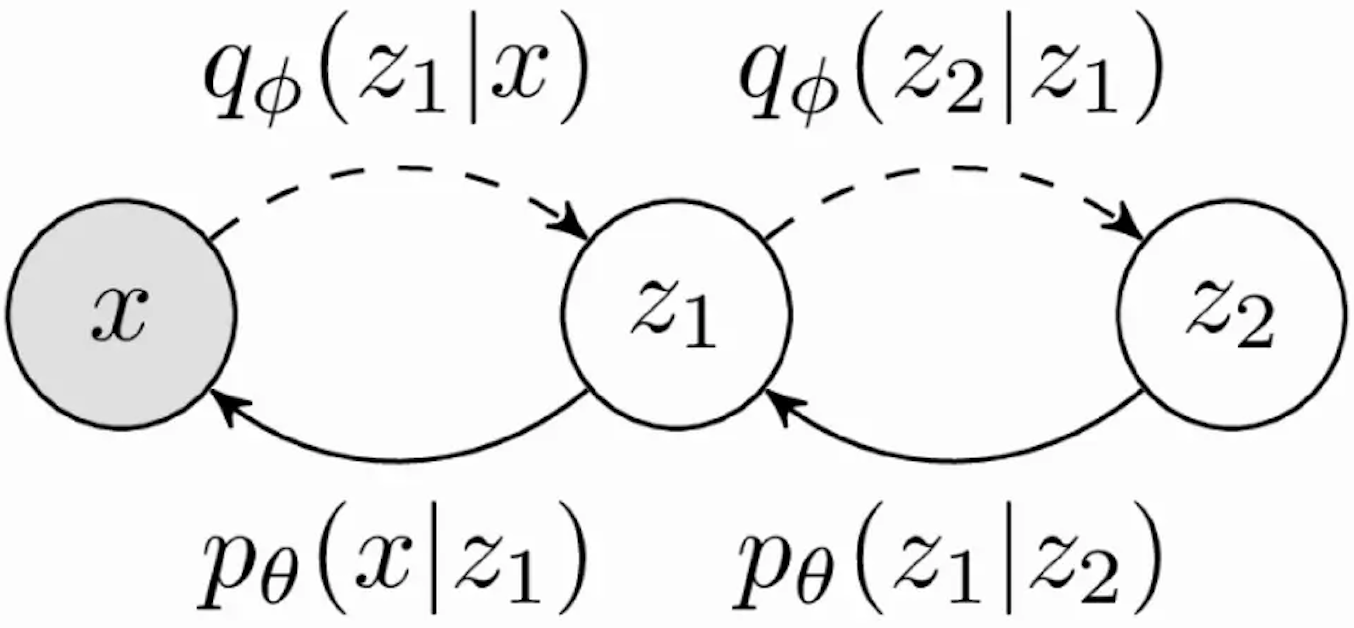
\[p(x) = \int_z p_\theta(x \mid z)p(z)\] \[p(x) = \int_z q_\phi(z \mid x) \frac{p_\theta(x \mid z) p(z)}{q_\phi(z \mid x)}\] \[\log p(x) = \log E_{z \thicksim q_\phi(z \mid x)}[\frac{p_\theta(x \mid z)p(z)}{q_\phi(z \mid x)}]\] \[\log p(x) \geq E_{z \thicksim q_\phi(z \mid x)}[\log \frac{p_\theta(x \mid z)p(z)}{q_\phi(z \mid x)}]\]

多层 VAE 的原理与变分下界

\[p(x) = \int_{z_1} \int_{z_2} p_\theta(x, z_1, z_2)d{z_1}, d{z_2}\] \[p(x) = \int_{z_1} \int_{z_2} q_{\phi}(z_1, z_2 \mid x) \frac{p_\theta(x, z_1, z_2)}{q_\phi(z_1, z_2 \mid x)}\] \[p(x) = E_{z_1, z_2 \thicksim q_\phi(z_1, z_2 \mid x)} [\frac{p_\theta(x, z_1, z_2)}{q_\phi(z_1, z_2 \mid x)}]\] \[\log p(x) \geq E_{z_1, z_2 \thicksim q_\phi(z_1, z_2 \mid x)} [\log \frac{p_\theta(x, z_1, z_2)}{q_\phi(z_1, z_2 \mid x)}]\] \[p(x, z_1, z_2) = p(x \mid z_1) p(z_1 \mid z_2) p(z_2)\] \[q(z_1, z_2 \mid x) = q(z_1 \mid x) q(z_2 \mid z_1)\] \[L(\theta, \phi) = E_{q(z_1, z_2 \mid x)}[\log p(x \mid z_1) - \log q(z_1 \mid x) + \log p(z_1 \mid z_2) - \log q(z_2 \mid z_1) + \log p(z_2)]\]

扩散过程 (Diffusion Process)

1、给定初始数据分布 $x_0 \thicksim q(x)$, 可以不断地向分布中添加高斯噪声，该噪声的标准差是通过固定值 $\beta_t$ 确定的，均值是以固定值 $\beta_t$ 和当前 $t$ 时刻的数据 $x_t$ 决定的。这个过程是一个马尔科夫链过程。 2、随着 $t$ 的不断增大，最终数据分布 $x_T$ 变成了一个各向独立的高斯分布。

给定一个从真实数据分布 $x_0 \thicksim q(x)$ 采样的数据点。定义一个前向扩散过程，其在 $T$ 个时间步添加少量高斯噪声到样本上，产生一个噪声样本序列 $x_1, …, x_T$。步长由一个方差时间表 ${\beta_t \in (0, 1)}_{t=1}^t$ 控制。

\[q(x_t \mid x_{t-1}) = N(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \quad q(x_{1...T} \mid x_0) = \prod_{t=1}^T q(x_t \mid x_{t-1}) \tag{1}\]

3、任意时刻的 $q(x_t)$ 推导可以完全基于 $x_0$ 和 $\beta_t$ 来计算出来，不需要做迭代

令 $\alpha_t = 1 - \beta_t$，通过重参数技巧，等式(1)可以写为：

\[\begin{aligned} x_t &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} z_{t-1} \\ &= \sqrt{\alpha_t} (\sqrt{\alpha_{t-1}} x_{t-2} + \sqrt{1- \alpha_{t-1}} z_{t-2}) + \sqrt{1 - \alpha_t} z_{t-1} \\ &= \sqrt{\alpha_t \alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}z_{t-2} + \sqrt{1 - \alpha_t} z_{t-1} \\ &= ... \\ &= \sqrt{\bar \alpha_t} x_0 + \sqrt{1 - \bar \alpha_t} z \end{aligned}\]

令 $\bar \alpha_t = \prod_{i=1}^T \alpha_i$：

\[q(x_t \mid x_0) = N(x_t; \sqrt{\bar \alpha_t}x_0, (1 - \bar \alpha_t)I)\]

Note：两个正态分布 $X \thicksim N(\mu_1, \sigma_1)$ 和 $Y \thicksim N(\mu_2, \sigma_2)$ 的叠加后的分布 $aX + bY$ 的均值 $a \mu_1 + b \mu_2$，方差为 $a^2 \sigma_1^2 + b^2 \sigma_2^2$ 。所以 $ \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}z_{t-2} + \sqrt{1 - \alpha_t} z_{t-1}$ 可以重参数化成一个只含一个随机变量 $z$ 构成的 $\sqrt{1 - \alpha_t \alpha_{t-1}}z$ 的形式。

逆扩散过程(Reverse Process)

逆扩散过程是从高斯噪声中恢复原始数据，可以假设它也是一个高斯分布，但是无法逐步地去拟合分布，所以需要构建一个参数分布去做估计。逆扩散过程仍然是一个马尔科夫链过程。

\[p_\theta(x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta(x_{t-1} \mid x_t) \quad p_\theta(x_{t-1} \mid x_t) = N(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))\]

后验的扩散条件概率 $q(x_{t-1} \mid x_t, x_0)$ 分布是可以用公式表达的，也就是说，给定 $x_t$ 和 $x_0$，可以计算出 $x_{t-1}$。

\[q(x_{t-1} \mid x_t, x_0) = N(x_{t-1}; \tilde \mu(x_t, x_0), \tilde \beta_t I)\]

使用贝叶斯规则，有：

\[\begin{align} q(x_{t-1} \mid x_t, x_0) &= \frac{q(x_t, x_{t-1}, x_0)}{q(x_t, x_0)} = \frac{q(x_t \mid x_{t-1}, x_0) q(x_{t-1} \mid x_0) q(x_0)}{q(x_t, x_0)} = q(x_t \mid x_{t-1}, x_0) \frac{q(x_{t-1} \mid x_0)}{q(x_t \mid x_0)} \\ &\propto \exp (- \frac{1}{2}(\frac{(x_t - \sqrt{\alpha_t} x_{t-1})^2}{\beta_t}) + \frac{(x_{t-1} - \sqrt{\bar \alpha_{t-1}}x_0)^2}{1 - \bar \alpha_{t-1}} - \frac{(x_t - \sqrt{\bar \alpha_t} x_0)^2}{1 - \bar \alpha_t})) \\ &= \exp(-\frac{1}{2}((\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar \alpha_{t-1}})x_{t-1}^2 - (\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar \alpha_t}}{1 - \bar \alpha_{t-1}}x_0)x_{t-1} + C(x_t, x_0))) \end{align}\]

Note: 高斯分布的概率密度函数是 $f(x) = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x - \mu)^2}{2 \sigma^2}}$

Note：$ax^2 + bx = a(x + \frac{b}{2a})^2 + C$

根据韦达定理：

\[\tilde \beta_t = 1 / (\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar \alpha_{t-1}}) = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_t} · \beta_t\] \[\tilde \mu_t(x_t, x_0) = (\frac{\sqrt{\alpha_t}}{\beta_t} x_t + \frac{\sqrt{\bar \alpha_t}}{1 - \bar \alpha_t}x_0) / (\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar \alpha_{t-1}}) = \frac{\sqrt{\alpha_t}(1 - \bar \alpha_{t-1})}{1 - \bar \alpha_t}x_t + \frac{\sqrt{\bar \alpha_{t-1}} \beta_t}{1 - \bar \alpha_t} x_0\]

根据 $x_0$ 和 $x_t$ 之间的关系式：

\[x_t = \sqrt{\bar \alpha_t} x_0 + \sqrt{1 - \bar \alpha_t} z\]

我们可以知道：

\[x_0 = \frac{1}{\sqrt{\bar \alpha_t}}(x_t - \sqrt{1 - \bar \alpha_t} z_t)\]

Q：既然 $x_{t}$ 可以通过 $x_0$ 和 $\beta$ 直接求出，那么$x_{t-1}$ 也应该可以直接求出，为什么要通过该种方式求出 $x_{t-1}$?

A：注意此时求的是后验概率 $q(x_{t-1} \mid x_{t}, x_0)$，这与 $q(x_{t-1} \mid x_0)$ 不同，因为 $q(x_{t-1})$ 和 $q(x_t)$ 并不是相互独立的。

Reference

Jascha Sohl-Dickstein, Eric Weiss, Niru Maheswaranathan, and Surya Ganguli. Deep unsupervised learning using nonequilibrium thermodynamics. In International Conference on Machine Learning, pages 2256–2265, 2015.
Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models[J]. Advances in Neural Information Processing Systems, 2020, 33: 6840-6851.
https://www.bilibili.com/video/BV1b541197HX/?spm_id_from=..search-card.all.click&vd_source=256546053d955f1315050ba88e6059c3

【深度学习】Diffusion Model