Background:ELBO,VAE,andHierarchicalVAE
对于许多模态,我们可以认为我们观察到的数据是由相关的看不见的隐变量表示或生成的,我们可以用随机变量 $z$ 表示。
Evidence Lower Bound
从数学上讲,我们可以想象通过联合分布建模的隐变量和我们观察到的数据 $p(x, z)$。 基于似然的生成模型是学习一个模型最大化所有观测 $x$ 的似然 $p(x)$。 我们有两种方法可以操纵这种联合分布以恢复纯粹我们观察到的数据 $p(x)$的似然; 我们可以显式地将隐变量 $z$ 边缘化(marginalize ):
\[p(x) = \int p(x, z) dz \tag{1}\]或者根据概率的链式法则:
\[p(x) = \frac{p(x, z)}{p(z \mid x)} \tag{2}\]直接计算并且最大化似然 $p(x)$ 是困难的, 因为在等式1中需要所有的隐变量 $z$ , 这在复杂的模型里是无迹可寻的, 或者在等式2中访问真实隐编码器 $p(z \mid x)$。 然而,使用这两个等式, 我们可以得到叫做 Evidence Lower Bound (ELBO) 的项。 在这种情况下,Evidence 被量化为观测数据的对数似然。然后,最大化 ELBO 成为优化隐变量模型的代理目标;在最好的情况下,当 ELBO 被参数化并完美优化时,它完全等同于 Evidence。形式上,ELBO的方程是:
\[E_{q_{\phi}(z \mid x)} [\log \frac{p(x, z)}{q_\phi(z \mid x)}] \tag{3}\]为了明确与 evidence 的关系,我们可以用数学书写:
\[\log p(x) \geq E_{q_{\phi}(z \mid x)}[\log \frac{p(x, z)}{q_\phi(z \mid x)}] \tag{4}\]$q_\phi(z \mid x)$ 是用参数 $\Phi$ 估计真实后验分布 $p(z \mid x)$ 的变分分布。 在 VAE 中,我们通过调整参数 $\Phi$ 增大下界以最大化 ELBO, 我们得到一个模型能够建模真实数据分布并从中采样, 因此我们学习了一个生成模型。现在, 让我们进一步理解为什么 ELBO 是我们想要最大化的目标。
使用等式1:
\[\begin{aligned} \log p(x) &= \log \int p(x, z)dz \quad &(应用等式 1) \quad &(5)\\ &= \log \int \frac{p(x, z) q_\phi(z \mid x)}{q_\phi(z \mid x)}dz \quad &(乘以 1 = \frac{q_\phi(z \mid x)}{q_\phi(z \mid x)}) \quad &(6) \\ &= \log E_{q_{\phi}(z \mid x)}[\frac{p(x, z)}{q_\phi(z \mid x)}] \quad &(期望的定义) \quad &(7) \\ &\geq E_{q_\phi(z \mid x)}[\log \frac{p(x, z)}{q_\phi(z \mid x)}] \quad &(应用 Jensen 不等式) \quad &(8) \end{aligned}\]这个证明无法在直觉上解释为什么 ELBO 是 evidence 的下界, 因为Jesen不等式没有告诉我们少的这部分是哪些东西。
用等式2推导:
\[\begin{aligned} \log p(x) &= \log p(x) \int q_\phi(z \mid x) dz \quad &(乘以 1 = \int q_\phi(z \mid x)dz) \quad &(9) \\ &= \int q_\phi(z \mid x)(\log p(x)) dz \quad &(将 evidence 引入 积分) \quad &(10) \\ &= E_{q_\phi(z \mid x)}[\log p(x)] \quad &(期望的定义) \quad &(11) \\ &= E_{q_\phi(z \mid x)}[\log \frac{p(x, z)}{p(z \mid x)}] \quad &(应用等式2) \quad &(12) \\ &= E_{q_\phi(z \mid x)}[\log \frac{p(x, z) q_\phi(z \mid x)}{p(z \mid x) q_\phi(z \mid x)}] \quad &(乘以 1 = \frac{q_\phi(z \mid x)}{q_\phi(z \mid x)}) \quad &(13) \\ &= E_{q_\phi(z \mid x)}[\log \frac{p(x, z)}{q_\phi(z \mid x)}] + E_{q_\phi(z \mid x)}[\log \frac{q_\phi(z \mid x)}{p(z \mid x)}] \quad &(拆分期望) \quad &(14) \\ &= E_{q_\phi(z \mid x)}[\log \frac{p(x, z)}{q_\phi(z \mid x)}] + D_{KL}(q_\phi(z \mid x) \| p(z \mid x)) \quad &(KL 散度的定义) \quad &(15) \\ &\geq E_{q_\phi(z \mid x)}[\log \frac{p(x, z)}{q_\phi(z \mid x)}] \quad &(KL 散度 \geq 0) \quad &(16) \end{aligned}\]从这个推导我们看到 evidence 等于 ELBO 加上估计的后验 $q_\phi(z \mid x)$ 和真正的后验 $p(z \mid x)$ 之间的 KL 散度。
首先,我们现在知道为什么ELBO确实是一个下限:evidence 和 ELBO 之间的差异是一个严格的非负的 KL 散度项,因此 ELBO 的值永远不会超过 evidence。
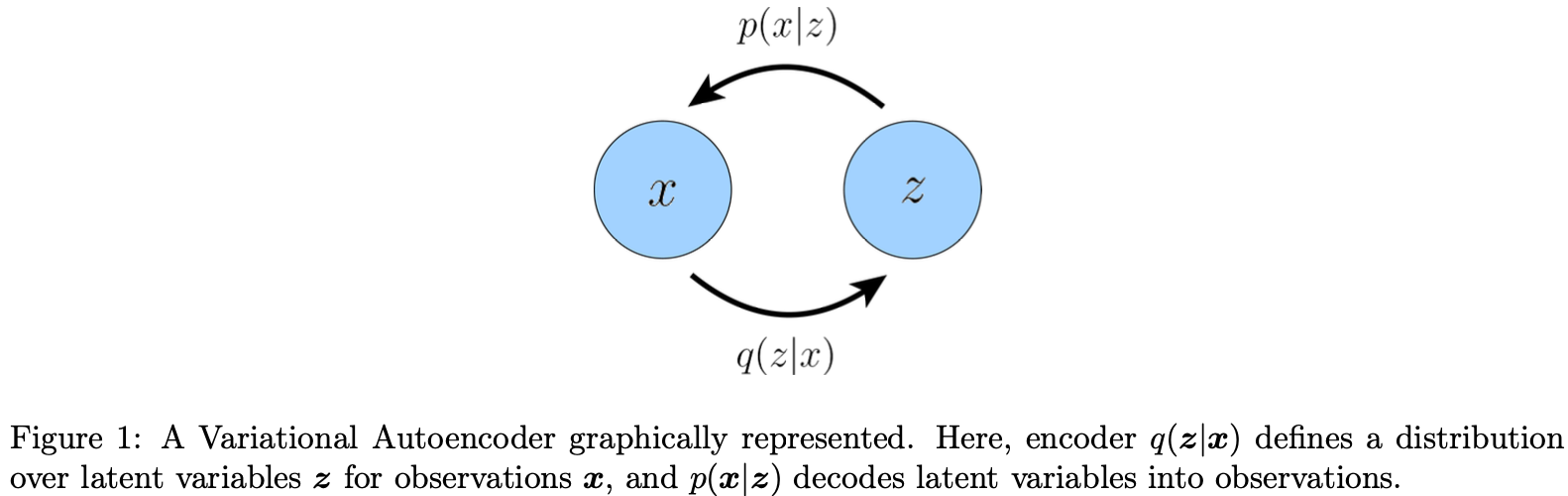
其次, 我们探索为什么我们想要最大化 ELBO。 我们想要优化变分后验 $q_\phi(z \mid x)$ 的参数来匹配真实的后验分布 $p(z \mid x)$, 这通过最小化它们的 KL 散度来实现。然而, 真实 $p(z \mid x)$ 分布是不知道的, 因此难以直接最小化 KL 散度。注意到等式15的左侧( evidence 项 $\log p(x)$ )总是一个常数, 因为它通过从联合分布 $p(x, z)$ 将所有隐变量 $z$ 边缘化计算得到的并且不依赖于参数 $\phi$。由于 ELBO 和 KL 散度的和是一个常数, 对应于参数 $\phi$, ELBO 的最大化等于 KL 散度项的最小化。因此, 对 $\phi$ 的 ELBO 的最大化作为如何完美建模真实隐后验分布的代理任务; 越优化 ELBO, 估计的后验分布越接近真实后验分布。此外, 一旦训练完成,ELBO 也可以用与估计观测或生成数据的似然, 因为它学习到了估计模型的 evidence $\log p(x)$。
Variational Autoencoders
VAE 的默认公式中, 我们直接最大化 ELBO。 这种方式叫做变分, 因为我们优化了 $\phi$ 参数化的潜在后验分布家族中的最佳 $q_\phi(z \mid x)$。它被称为自编码器,因为它让人想起传统的自编码器模型,在经历了中间瓶颈表示步骤后,输入数据被训练以预测自己。为了明确这种联系,让我们进一步剖析 ELBO 项:
\[\begin{aligned} E_{q_\phi(z \mid x)} [\log \frac{p(x, z)}{q_\phi(z \mid x)}] &= E_{q_\phi(z \mid x)}[\log \frac{p_\theta(x \mid z)p(z)}{q_\phi(z \mid x)}] \\ &= E_{q_\phi(z \mid x)}[\log p_\theta(x \mid z)] + E_{q_\phi(z \mid x)}[\log \frac{p(z)}{q_\phi(z \mid x)}] \end{aligned}\]Hierarchical Variational Autoencoders
-
Previous
【深度学习】Sovling Inverse Problems in Medical Imaging with Score-Based Generative Models -
Next
【深度学习】CenterMask : Real-Time Anchor-Free Instance Segmentation