Abstract
最近关于即插即用图像恢复的工作表明,去噪器可以隐式地作为基于模型的方法解决许多逆问题的先验图像。
当通过具有大建模能力的深度卷积神经网络(CNN)进行判别式学习时,这种属性为即插即用图像恢复带来了相当大的优势(例如,集成了基于模型的方法的灵活性和基于学习的方法的有效性)。
然而,虽然更深和更大的CNN模型正在迅速流行,但由于之前缺乏合适的去噪器先验,现有的即插即用图像恢复阻碍了其性能。
为了突破即插即用图像恢复的极限,我们通过训练高度灵活和有效的 CNN 去噪器,事先建立了一个基准深度去噪器。
然后,我们将深去噪器作为模块化部分插入基于半二次分裂的迭代算法,以解决各种图像恢复问题。
与此同时,我们对参数设置、中间结果和经验收敛进行了彻底的分析,以更好地了解工作机制。
三个具有代表性的图像恢复任务的实验结果表明,包括去模糊、超分辨率和去马赛克,所提出的带有深度去噪器的即插即用图像恢复不仅明显优于其他最先进的基于模型的方法,而且与最先进的基于学习的方法相比,实现了有竞争力甚至更优越的性能。源代码:https://github.com/cszn/DPIR 。
Introduction
图像恢复(IR)一直是一个长期存在的问题,因为它在各种低级视觉应用中具有高度的实用价值。一般来说,图像恢复的目的是从退化的观测 $y = Ax + n$ 中恢复潜在的干净图像 $x$, 其中 $A$ 是和噪声相关的退化操作, $n$ 是具有标准差为 $\sigma$ 的加性高斯白噪声。通过指定不同的退化操作,可以相应地获得不同的 IR 任务。当 $A$ 是恒等操作时,典型的 IR 任务是图像去噪; 当T是二维卷积操作时,典型的IR任务是图像去模糊,当T是卷积和向下采样的复合操作时,典型的IR任务是图像超分辨率,当T是彩色滤波器阵列(CFA)屏蔽操作时,典型的 IR 任务是彩色图像去马赛克。
由于IR是一个病态的逆问题,因此需要采用也称为正则化的先验问题来约束解空间。从贝叶斯的角度来看,可以通过求解最大后验(MAP)估计问题来获得解 $\hat x$,
\[\hat x = \text{arg} \max_x \log p(y \mid x) + \log p(x) \tag{1}\]其中 $\log p(y \mid x)$ 表示观测 $y$ 的对数似然, $\log p(x)$ 提供干净图像的先验并且独立于退化图像 $y$。更正式地, (1) 可以重新公式化为:
\[\hat x = \text{arg} \min_x \frac{1}{2\sigma^2} \| y - Ax \|^2 + \lambda R(x) \tag{2}\]其中解为最小化数据保真项 $\frac{1}{2 \sigma^2} | y - Ax |^2$ 的能量函数以及正则项 $\lambda R(x)$。 具体来说,数据项保证解案符合退化过程,而先验项通过在解上强制施加所需属性来缓解病态度。
一般来说,解决等式(2)的方法可以分为两大类,即基于模型的方法和基于学习的方法。前者旨在用一些优化算法直接解决等式(2),而后者主要通过在包含 $N$ 个退化-干净图像对的训练集上优化损失函数来训练截断展开推理。特别是,基于学习的方法通常被建模为以下双级优化问题
\[\begin{cases} \min_\Theta \sum_{i=1}^N L(\hat x_i, x_i) \\ s.t. \quad \hat x_i = \text{arg} \min_x \frac{1}{2\sigma^2}\|y_i - Ax\|^2 + \lambda R(x) \end{cases} \tag{3}\]其中 $\Theta$ 表示可训练的参数, $L(\hat x_i, x_i)$ 测量估计的干净 $\hat x_i$ 和真实图像 $x_i$ 之间的距离。通过将展开推理 3(b)替换为一个预定义的函数 $\hat x = f(y, \Theta)$, 我们可以将朴素的基于学习的方法视为广义的公式(3)。
$t$ 很容易注意到,基于模型的方法和基于学习的方法之间的一个主要区别是,前者可以灵活地通过简单地指定 A 来处理各种 IR 任务,并且可以直接对退化的图像 $y$ 进行优化,而后者在测试前需要繁琐的训练来学习模型,并且通常受到特定任务的限制。尽管如此,基于学习的方法不仅可以享受快速的测试速度,而且由于端到端的训练,它往往会提供更好的性能。相比之下,基于模型的方法通常很耗时,有复杂的先验,以达到良好的表现。因此,这两类方法有其各自的优点和缺点,因此,利用其各自优点来调查它们的整合将是有吸引力的。这种集成导致了深度即插即用IR方法,该方法用基于学习的CNN去噪器取代了基于模型的优化的去噪子问题。
深度即插即用IR的主要思想是,借助变量分裂算法,如 alternating direction method of multipliers(ADMM)[11]和 half-quadratic splitting(HQS)[12],可以分别处理数据项和先验项[13],特别是,先验项只对应于去噪子问题[14],[15],[16],可以通过深度CNN去噪器解决。虽然已经提出了几项深度即插即用 IR 作品,但它们通常存在以下缺点。首先,他们要么采用不同的去噪器来覆盖广泛的噪声水平,要么使用在一定噪声水平上训练的单个去噪器,这不适合解决去噪子问题。例如,IR-CNN [17] denoisers涉及25个独立的7层denoisers,每个denoisers的间隔噪声水平为2。其次,他们的Denoisers 不够强大,因此,深即插即用 IR 的性能极限尚不清楚。第三,缺乏对其工作机制的深刻实证理解。
本文是我们之前工作[17]的延伸,采用更灵活、更强大的深度CNN去噪器,旨在通过对不同的 IR 任务进行广泛的实验来突破深度即插即用 IR 的极限。具体来说,受FFDNet[18]的启发,所提出的深度去噪器可以通过以噪声水平图为输入,通过单个模型处理广泛的噪声水平。此外,通过利用ResNet[19]和U-Net[20]来提高其有效性。深层去噪器被进一步纳入基于 HQS 的即插即用 IR 中,以显示使用强大的深层去噪器的优点。与此同时,提出了一种新的periodical geometric self-ensemble,在不引入额外计算负担的情况下提高性能,并提供对参数设置、中间结果和经验结合的透彻分析,以更好地了解所提出的深度即插即用 IR 的工作机制。
这项工作的贡献总结如下:
- 训练有灵活而强大的深度CNN去噪器。它不仅优于最先进的深度高斯去噪模型,而且适合解决即插即用 IR。
- 在参数设置、中间结果和实证收敛方面,对基于 HQS 的即插即用 IR 进行了彻底分析,从而更好地了解了工作机制。
- 关于去模糊、超分辨率和去马赛克的广泛实验结果表明,所提粗的即插即用 IR 与深度去噪器的优越性。
Related Works
Difference to Deep Unfolding IR
应该注意的是,除了即插即用 IR 外,深度展开 IR 还可以结合基于模型的方法和基于学习的方法的优势。它们之间的主要区别在于,后者将截断的展开优化解释为端到端可训练的深度网络,因此通常以更少的迭代产生更好的结果。然而,深度展开的 IR 需要对每项任务进行单独的训练。相比之下,无需此类额外训练,即插即用 IR 很容易部署。
HQS Algorithm for Plug-and-Play IR
尽管存在各种即插即用 IR 的变量拆分算法,但 HQS 的受欢迎程度归功于简单性和快速收敛。因此,我们在本文中采用了HQS。另一方面,毫无疑问,参数设置始终是一个不平凡的问题[37]。换句话说,需要仔细的参数设置才能获得良好的性能。为了更好地了解基于 HQS 的即插即用 IR,我们将在提供 HQS 算法后讨论参数设置的一般方法。然后,我们提出了一个 periodical geometric self-ensemble 策略,以提高性能。
Half Quadratic Splitting (HQS) Algorithm
为了解耦(2)的数据项和先验项,HQS 首先引入了一个辅助变量 $z$,导致有约束的优化问题:
\[\hat x = \text{arg} \min_x \frac{1}{2\sigma^2}\| y - Ax \|^2 + \lambda R(z) \qquad \text{s.t.} \qquad z = x. \tag{4}\]上式可以通过最小化如下问题求解:
\[L_\mu(x, z) = \frac{1}{2\rho^2} \| y - Ax \|^2 + \lambda R(z) + \frac{\mu}{2}\|z - x\|^2 \tag{5}\]其中 $\mu$ 是惩罚参数。这个问题可以通过迭代解决 $x$ 和 $z$ 的以下子问题来解决,同时保持其余变量的固定,
\[\begin{cases} x_k = \text{arg} \min_x \|y - Ax \|^2 + \mu \sigma^2\|x - z_{k-1}\|^2 \\ z_k = \text{arg} \min_z \frac{1}{2(\sqrt{\lambda / \mu})} \| z - x_k \|^2 + R(z) \end{cases} \tag{6}\]因此,数据项和先验项被解耦成两个单独的子问题。具体来说,(6a) 的子问题目标是找到 $z_{k-1}$ 的近端点, 通常根据 A 有闭式解, 而 (6b) 的子问题从贝叶斯视角对应一个噪声规模为 $\sqrt{\lambda / \mu}$ 在 $x_k$ 上的高斯去噪。因此,高斯去噪器可以插入交替迭代求解 (2)。 为了解决这个问题, 我们重写 (6b) 如下:
\[z_k = Denoiser(x_k, \sqrt{\lambda / \mu}) \tag{7}\]一个人可以从(7)获得两个观察结果。首先,先验的 $R(·)$ 可以由去噪器隐式指定。因此,即插即用 IR 的先验和去噪器通常被称为去噪器先验。其次,学习一个CNN去噪器来取代(7)很有趣,以便利用CNN的优势,例如网络设计的高灵活性、GPU的高效率和具有深度网络的强大建模能力。
General Methodology for Parameter Setting
从(6a)和(6b)之间的交替迭代中,很容易看出涉及三个可调参数,包括惩罚参数 $\mu$、正则化参数 $\lambda$ 和迭代总数 $K$。
为了保证 $x_k$ 和 $z_k$收敛在一个固定点, 需要一个大的 $\mu$, 其需要一个大的 $K$ 收敛。因此,常见的方式是逐渐增加 $\mu$, 导致一系列 $\mu_1 < … < \mu_k < … < \mu_K$ 。 然而,需要引入一个新的参数来控制步长,使参数设置更加复杂。根据(7), 我们可以滚查到 $\mu$ 控制去噪先验第 $k$ 个迭代的噪声规模 $\sigma_k(\triangleq \sqrt{\lambda / \mu_k})$。 另一方面,[0, 50]的噪音水平范围应该足以满足 $\sigma_k$。 受这种领域知识的启发,我们可以设置 $\sigma_k$ 和 $\lambda$ 来隐式确定 $\mu_k$。基于 $\mu_k$ 应该单调增长的事实,我们在对数空间中将 $\sigma_k$ 从大噪声级 $\sigma_1$ 均匀采样到小的 $\sigma_K$。这意味着 $\mu_k$ 可以轻易通过 $\mu_k = \lambda / \sigma_k^2$ 确定。 $\sigma_1$ 固定为49, $\sigma_K$ 由图像噪声规模 $\sigma$ 决定。 由于 $K$ 是用户指定的, $\sigma_K$ 有明确的物理意义, 它们易于设定。
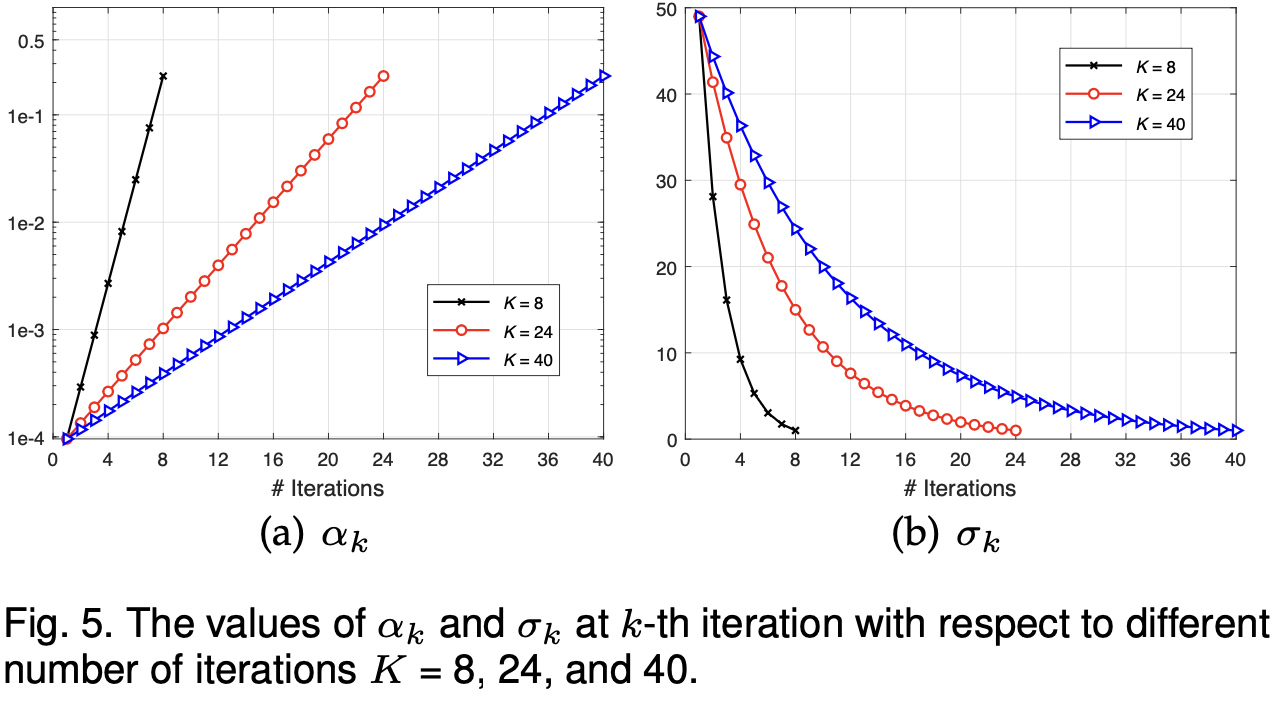
到目前为止,剩余的设置参数是 $\lambda$。 由于 $\lambda$ 来自先验项,因此应该是固定的,我们可以通过在验证数据集上的网格搜索来选择最佳 $\lambda$。从经验上讲,$\lambda$ 可以从 [0.19, 0.55] 范围内产生良好的性能。 在本文中,除非另有说明,否则我们将其固定为0.23。应该注意的是,由于 $\lambda$ 可以被吸收到$\sigma$ 中,并起到控制数据项和先验项项之间权衡的作用,因此可以通过将 $\sigma$ 乘以标量来隐式调整 $\lambda$。为了更清楚理解参数设定,设置 $\alpha_k \triangleq \mu_k \sigma^2 = \lambda \sigma^2 / \sigma_k^2$ 并且假设 $\sigma_K = \sigma = 1$, 我们绘制了对应于不同迭代数目K=8, 24 和 40 的 $\alpha_k$ 和 $\sigma_k$ 值。
-
Previous
【深度学习】Deep Unfolding, Diffusion Model and CASSI -
Next
【深度学习】MAE_ST:Masked Autoencoders As Spatiotemporal Learners