Abstract
从数据中创建噪声很容易;从噪声中创建数据是生成建模。
这篇文章提出了一个随机微分方程(SDE),通过缓慢注入噪声将复合数据分布平稳转换为已知的先验分布,以及相应的反向时间SDE,通过缓慢消除噪声将先验分布转换回数据分布。
至关重要的是,反向时间 SDE 仅取决于扰动数据分布的时间依赖梯度场(又名分数)。
通过利用基于分数的生成建模的进步,可以使用神经网络准确估计这些分数,并使用数值SDE求解器生成样本。
作者表明,该框架概括了以前基于分数的生成建模和扩散概率建模的方法,使得新的采样程序和新的建模能力。
特别是,作者引入了一个预测器-校正器框架,以纠正离散反向时间SDE演变中的错误。
作者还推导出了等效的神经ODE,该样本来自与SDE相同的分布,但还实现了精确的似然计算,并提高了采样效率。
此外,作者提供了一种解决基于分数的模型反向问题的新方法,如类条件生成、图像绘画和着色实验所证明的那样。
结合多种架构改进,作者在CIFAR-10上实现了无条件图像生成的破纪录性能,Inception score 为 9.89,FID为2.20,competitive likelihood 为2.99 bits/dim,并首次从基于分数的生成模型中演示了 $1024 \times 1024$ 图像的高保真生成。
Introduction
两类成功的概率生成模型涉及以缓慢增加的噪声顺序损坏训练数据,然后学习扭转这种损坏,以生成数据。Score matching with Langevin dynamics (SMLD) 在每个噪声尺度估计 score (数据对数概率密度的梯度), 然后在生成过程中使用郎之万采样从一系列离散噪声尺度中采样样本。Denoising diffusion probabilistic modeling (DDPM) 训练一系列概率模型逆转噪声损坏的每一步,使用你分部的函数形式的知识使得训练可追溯。对于连续状态空间,DDPM 训练目标隐式计算每个噪声尺度的分数。因此,将这两个模型类称为基于分数的生成模型。
基于分数的生成模型和相关技术已被证明在生成图像、音频、图形和形状方面是有效的。为了启用新的采样方法并进一步扩展基于分数的生成模型的能力,作者提出了一个统一的框架,通过随机微分方程(SDE)泛化之前的方法。
具体来说,作者考虑的是,根据扩散过程随着时间的推移而演变的连续分布,而不是用有限数量的噪声分布扰动数据。这个过程逐渐将数据点扩散到随机噪声中,并由指定的 SDE 给出,该 SDE 不依赖于数据,也没有可训练参数。通过逆转这个过程,我们可以将随机噪声平稳地塑造成数据,以便生成样本。至关重要的是,这个反向过程满足反向时间 SDE,将边缘概率密度作为时间函数的分数,可以从前向SDE导出。因此,我们可以通过训练时间依赖的神经网络来估计分数,然后使用数值 SDE 求解器生成样本,来近似反向时间 SDE。关键思想总结为图1。

作者提议的框架有几个理论和实践贡献:
Flexible sampling and likelihood computation: 使用任何通用 SDE solver 来集成反向时间 SDE 进行采样。此外,作者提出了两种对一般 SDE 不可行的特殊方法:(i) Predictor-Corrector (PC) 将数 值SDE求解器与基于分数的MCMC 方法相结合的采样器,如 Langevin MCMC 和 HMC;(ii) 基于概率流常微分方程(ODE)的确定性采样器。前者统一并改进了基于分数的模型的现有采样方法。后者允许通过黑盒ODE求解器进行快速自适应采样,通过隐编码进行灵活的数据操作,唯一可识别的编码,特别是精确的似然计算。
Controllable generation: 我们可以使用训练期间不可用的信息控制生成过程,因为条件反向时间 SDE 可以从无条件分数中有效地估计。这使类条件生成、图像绘制、着色和其他逆问题等应用程序都能够实现,所有这些都可以使用单个无条件的基于分数的模型实现,而无需重新训练。
Unified framework: 该框架提供了探索和调整各种SDE的统一方式,以改进基于分数的生成模型。SMLD 和 DDPM 的方法可以合并到该框架中,作为两个独立的 SDE 的离散化。尽管最近据报道 DDPM的样本质量高于SMLD,但作者表明,该框架允许的更好的架构和新的采样算法,SMLD可以赶上DDPM——它实现了CIFAR-10上新的最先进的Inception Score(9.89)和 FID Score(2.20),以及首次从基于分数的模型中高保真生成 $1024 \times 1024$ 图像。
Background
Denoising Score Matching With Langevin Dynamics (SMLD)
令 $p_{\sigma}(\tilde x \mid x) := N(\tilde x; x, \sigma^2 I)$ 表示一个扰动核, $p_{\sigma}(\tilde x) := \int p_{data}(x) p_{\sigma}(\tilde x \mid x)dx$, 其中 $p_{data}(x)$ 表示数据分布。考虑一个正噪声尺度的序列 $\sigma_{min} = \sigma_1 < \sigma_2 < … < \sigma_N = \sigma_{max}$。 通常, $\sigma_{min}$ 足够小, 有 $p_{\sigma_{min}}(x) \approx p_{data}(x)$, $\sigma_{max}$足够大, 有 $p_{\sigma_{max}} \approx N(x; 0, \sigma_{max} I)$。 Song&Ermon(2019) 等人提出一个 Noise Conditional Score Network (NCSN), 表示为 $s_{\theta}(x, \sigma)$ , 其使用去噪分数匹配的加权和作为目标函数:
\[\theta^* = \arg \min_{\theta} \sum_{i=1}^N \sigma_i^2 E_{p_{data}(x)}E_{p_{\sigma_i(\tilde x \mid x)}} [\| s_{\theta}(\tilde x, \sigma_i) - \nabla_{\tilde x} \log p_{\sigma_i}(\tilde x \mid x) \|_2^2]\]给定足够的数据和模型容量,对于 $\sigma \in {\sigma_i}{i=1^N}$ 最优的基于分数的模型 $s{\theta^*}(x, \sigma)$ 几乎在所有位置上匹配到 $\nabla_x \log p_{\sigma}(x)$。 为了采样, Song & Ermon (2019) 为每个 $p_{\sigma_i}(x)$ 运行 Langevin MCMC M 步。
\[x_i^m = x_i^{m-1} + \epsilon_i s_{\theta^*}(x_i^{m-1}, \sigma_i) +\sqrt{2 \epsilon_i} z_i^m, m = 1, 2, ..., M\]其中 $\epsilon_i > 0$ 是步长,$z_i^m$ 是标准正态分布。
Denoising Diffusion Probabilistic Models (DDPM)
Sohl-Dickstein et al. (2015); Ho et al. (2020) 考虑一个正噪声尺度 $0 < \beta_1, \beta_2, …, \beta_N < 1$ 。 对于每个训练数据点 $x_0 \thicksim p_{data}(x)$, 构造一个离散马尔科夫链 ${x_0, x_1, …, x_N}$ , 因此 $p(x_i \mid x_{i-1}) = N(x_i; \sqrt{1-\beta_i}x_{i-1}, \beta_i I)$, 可以推导得到 $p_{\alpha_i}(x_i \mid x_0) = N(x_i; \sqrt{\bar \alpha_i}x_0, (1- \bar \alpha_i) I)$, 其中 $\bar \alpha_i := \prod_{j=1}^i (1 - \beta_j)$。 类似于 SMLD, 我们可以表示扰动数据分布为 $p_{\alpha_i}(\tilde x) := \int p_{data}(x)p_{\alpha_i}(\tilde x \mid x)dx$。 规定噪声尺度使得 $x_N$ 分布接近 $N(0, I)$。 一个变分马尔科夫链逆过程被参数化为 $p_\theta(x_{i-1} \mid x_i) = N(x_{i-1}; \frac{1}{\sqrt{1 - \beta_i}}(x_i + \beta_i s_\theta(x_i, i)), \beta_i I)$, 并且用一个重加权的变分下界训练 :
\[\theta^* = \mathop{\text{argmin}}_\theta \sum_{i=1}^N (1 - \alpha_i) E_{p_{data}(x)} E_{p_{\alpha_i(\tilde x \mid x)}]}[\|s_\theta(\tilde x, i) - \| \nabla_{\tilde x} \log p_{\alpha_i}(\tilde x \mid x) \|_2^2] \tag{3}\]在求解 Eq.(3) 后得到最优模型 $s_{\theta^*}(x, i)$ , 样本可以从 $X_N \thicksim N(0, I)$ 采样生成, 接下来按如下估计逆马尔科夫链:
\(x_{i-1} = \frac{1}{\sqrt{1 - \beta_i}}(x_i + \beta_i s_{\theta^*}(x_i, i)) + \sqrt{\beta_i} z_i, \quad i = N, N-1, ..., 1 \tag{4}\) Note: 该项的推导来自于重参数技巧 $x_t = \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} z_t $.
作者称这种方式为 ancestral sampling, 因为它相当于从图模型 $\prod_{i=1}^N p_\theta(x_{i-1} \mid x_i)$ 中执行祖先采样。Eq.(1) 和 Eq.(3) 的目标都是去噪分数匹配目标的加权和, 这表明最优的模型 $s_{\theta^*}(\tilde x, i)$ 匹配扰动数据分布的分数 $\nabla_x \log p_{\alpha_i}(x)$。 值得注意的是, Eq.(1) 和 Eq.(3) 的权重, 也就是 $\sigma_i^2$ 和 $(1 - \alpha_i)$ 与以相同的形式与扰动核相关: $\sigma_i^2 \propto E[| \nabla_x \log p_{\sigma_i} (\tilde x \mid x) |2^2]$ 和 $(1 - \alpha_i) \propto 1 / E[| \nabla_x \log p{\alpha_i}(\tilde x \mid x)|_2^2]$。
Score-Based Generative Mideling With SDEs
具有多个噪声尺度的扰动数据是之前方法成功的关键。作者建议将这个想法进一步推广到无限数量的噪声尺度,以便扰动的数据分布随着噪声的加剧而根据SDE进行演变。框架的总览如图2所示。
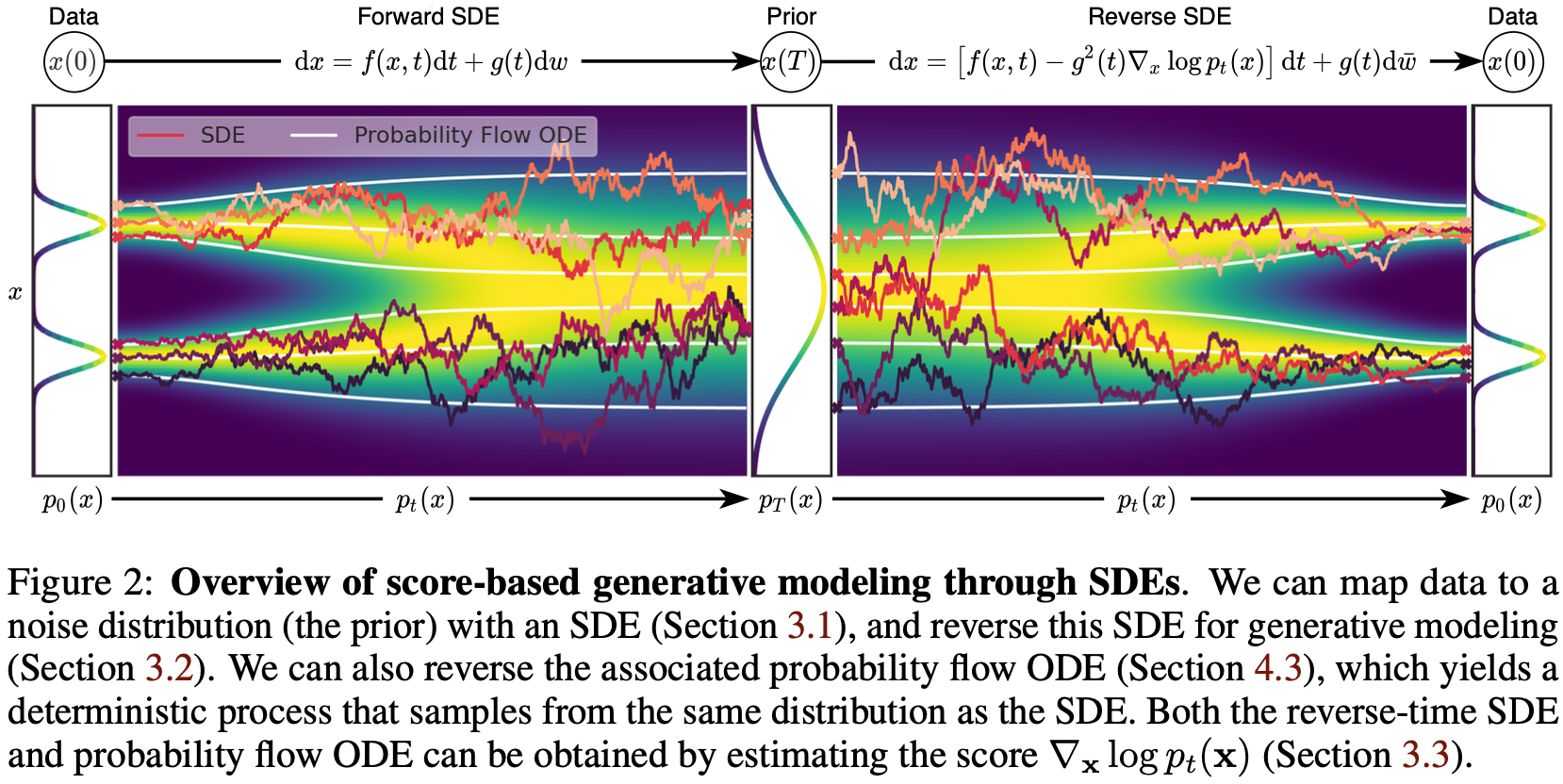
Perturbing Data With SDEs
我们的目标是构建一个扩散过程 ${x(t)}_{t=0}^T$ 通过一个连续时间变量 $t \in [0, T]$ 索引, 例如 $x(0) \thicksim p_0$ 和 $x(T) \thicksim p_T$。 $p_0$ 是数据分布, $p_T$ 是先验分布。 扩散过程可以被建模为 SDE 的解:
\[dx = f(x, t) dt + g(t) dw \tag{5}\]其中 $w$ 是标准 Wiener 过程, $f(·, t): R^d \rightarrow R^d$ 是 vector-value 函数, 叫做 $x(t)$ 的 drift 系数, $g(·): R \rightarrow R$ 是标量函数,叫做 $x(t)$ 的 diffusion 系数。为了便于陈述,我们假设扩散系数是一个标量,并且不依赖于 $x$,但我们的理论可以推广到在这些情况下成立(见附录A)。只要系数在状态和时间上都是全局 Lipschitz,SDE就有一个唯一的强解。我们这里将 $p_t(x)$ 表示为 $x(t)$ 的概率密度, 使用 $p_{st}(x(t) \mid x(s))$ 表示从 $x(s)$ 到 $x(t)$ 的 transition kernel, 其中 $0 \leq s < t \leq T$。
通常,$p_T$ 是未构造的先验分布, 其不包含 $p_0$ 的信息, 例如是一个固定均值和方差的高斯分布。构造 Eq.(5) 中的 SDE 有多种方式, 其将数据分布扩散到固定的先验分布。
Generating Samples by Reversing the SDE
通过从 $x(T) \thicksim p_T$ 采样和逆过程, 我们可以得到样本 $x(0) \thicksim p_0$。 Anderson(1982)的一个显著结果表明,扩散过程的逆过程也是一个扩散过程,在时间上向后运行,并由反向时间 SDE 给出:
\[dx = [f(x, t) - g(t)^2 \nabla_x \log p_t(x)]dt + g(t)d \bar w \tag{6}\]其中 $\bar w$ 是标准 Wiener 过程,时间从 $T$ 流向 $0$, $dt$ 是无穷小的负时间步。一旦得到每个时间 $t$ 的边缘分布的分数 $\nabla_x \log p_t(x)$, 我们可以得到 Eq.(6) 的逆扩散过程, 并仿真它从 $p_0$ 采样。
Estimating Scores for the SDE
分布的 score 可以通过在样本上用 score matching 训练一个 score-based 模型来估计。 为了估计 $\nabla_x \log p_t(x)$, 我们可以通过连续泛化 Eqs.(1) 和 (3) 训练一个时间依赖的基于分数的模型 $s_\theta(x, t)$ :
\[\theta^* = \arg \min_\theta E_t \{\lambda(t) E_{x(0)} E_{x(t) \mid x(0)}[\|s_\theta(x(t), t) - \nabla_{x(t)} \log p_{0t}(x(t) \mid x(0)) \|_2^2] \} \tag{7}\]这里 $\lambda : [0, T] \rightarrow R_{>0}$ 是正加权函数, $t$ 在 $[0, T]$ 上均匀采样, $x(0) \thicksim p_0(x)$ 和 $x(t) \thicksim p_{0t}(x(t) \mid x(0))$。 有足够的数据和模型容量, score matching 确保 Eq. (7) 的最优解 $s_{\theta^*}(x, t)$ 等于 $\nabla_x \log p_t(x)$。 在 SMLD 和 DDPM 中, 我们可以选择 $\lambda \propto 1 / E[| \nabla_{x(t)} \log p_{0t}(x(t) \mid x(0))|_2^2]$。 虽然 Eq. (7) 使用去噪分数匹配, 但是其他分数匹配目标也可以应用。
我们通常需要知道 transition kernel $p_{0t}(x(t) \mid x(0))$ 来求解 Eq. (7)。 当 $f(·, t)$ 近似, transition kernel 总是一个高斯分布, 其中均值和方差是以闭式解的形式已知的, 并且我们可以通过标准技术得到。 对于更一般的 SDEs, 我们可以求解 Kolmogorov 前向方程来得到 $p_{0t}(x(t) \mid x(0))$。 或者,我们可以从 $p_{0t}(x(t) \mid x(0))$ 中采样来仿真 SDE, 并替换 Eq. (7) 的去噪分数匹配为 sliced score matching 用与建模训练, 其绕过了 $\nabla_{x(t)} \log p_{0t} (x(t) \mid x(0))$ 的计算。
Examples: VE, VP SDEs and Beyond
SMLD 和 DDPM 中使用的噪声扰动可以被视为两种不同 SDE 的离散化。
当使用总共 $N$ 个噪声尺度, SMLD 对应 $x_i$ 的分布的的扰动核 $p_{\sigma_i} (x \mid x_0)$ 遵循下面的马尔科夫链:
\[x_i = x_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2} z_{i-1} \quad i = 1, ..., N \tag{8}\]其中 $z_{i-1} \thicksim N(0, I)$ , 我们引入 $\sigma_0 = 0$ 来简化表达。当有限的 $N \rightarrow \infty$, ${\sigma_i}{i=1}^N$ 变成一个函数 $\sigma(t)$, $z_i$ 变成 $z(t)$, 马尔科夫链 ${x_i}{i=1}^N$ 变成一个连续随机过程 ${x(t)}{t=1}^1$, 这里我们使用一个连续时间变量 $t \in [0, 1]$ 用于索引, 而不是一个整数 $i$。 ${x(t)}{t=0}^1$ 由以下的 SDE 给定:
\[dx = \sqrt{d[\sigma^2(t)]}{dt} dw \tag{9}\]DDPM 的扰动核 ${p_{\alpha_i}(x \mid x_0)}_{i=1}^N$ 类似, 离散马尔科夫链为:
\[x_i = \sqrt{1 - \beta_i} x_{i-1} + \sqrt{\beta_i} z_{i-1}, \quad i=1, ..., N \tag{10}\]当 $N \rightarrow \infty$, Eq. (10) 收敛到下列SDE
\[dx = -\frac{1}{2} \beta(t) x dt + \sqrt{\beta(t)} dw \tag{11}\]因此 SMLD 和 DDPM 中使用的噪声扰动对应于 Eqs. (9) 和 (11) 中的 SDEs 的离散化。有趣的是, Eq. (9) 的 SDE 当 $t \rightarrow \infty$ 总是方差爆炸, 而 Eq. (11) 当初始分布为单位方差产生固定的方差。由于这种差异, 我们将 Eq. (9) 叫做 Variance Exploding (VE) SDE, Eq. (11) 叫做 Variance Preserving (VP) SDE。
受到 VP SDE 的启发, 作者提出一种新型的 SDEs, 其在似然上表现地很好:
\[dx = -\frac{1}{2} \beta(t)xdt + \sqrt{\beta(t)(1 - e^{-2 \int_0^t \beta(s)ds})} dw \tag{12}\]当使用相同的 $\beta(t)$ 并且从相同的初始分布开始, 在每个中间时间步 Eq. (12) 的随机过程总是以 VP SDE 为界。由于这个原因,我们叫 Eq. (12) 为 sub-VP SDE。
因为 VE, VP 和 sub-VP SDEs 都有相似的漂移系数, 他们的扰动核 $p_{0t}(x(t) \mid x(0))$ 都是高斯分布, 并且可以以闭式解的形式计算。
Solving the Reverse SDE
在训练一个时间依赖的基于分数的模型 $s_\theta$ 后, 我们可以使用它构造反向时间 SDE 并且用数值方式仿真它来从 $p_0$ 生成样本。
General-purpose Numerical SDE Solvers
数值求解器提供来自SDE的近似轨迹。存在许多求解 SDE 的通用数值方法,例如 Euler-Maruyama 和 stochastic Ruge-Kutta方法(Kloe-den和Platen,2013年),它们对应于随机动力学的不同离散化。我们可以将其中任何一个应用于反向时间 SDE 进行样本生成。
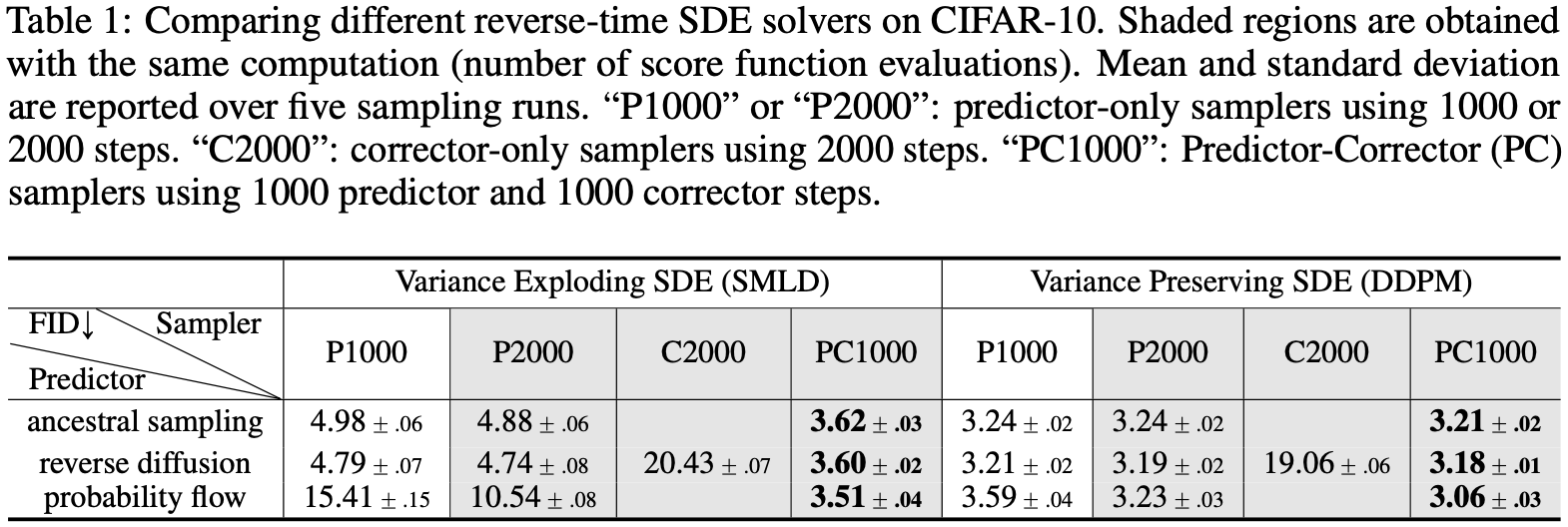
Ancestral sampling, DDPM 的采样方法 (Eq. (4)), 实际上对应着一个反向时间 VP SDE (Eq. (11)) 的一个特殊离散情况。 然而,为新的 SDE 推导出 ancestral sampling 规则可能并不简单。为了解决这个问题,作者提出了 reverse diffusion samplers(详见附录E),它以与前向采样相同的方式离散反向时间SDE,因此在前向离散化的情况下可以很容易地推导出。如表1所示,在 CIFAR-10 上,SMLD 和 DDPM 模型的反向扩散采样器的表现都略好于 ancestral sampling(DDPM型 ancestral sampling 也适用于 SMLD 模型,见附录F)。
Predictor-Corrector Samplers
与通用 SDE 不同,我们还有其他可以改进解的信息。由于我们有一个基于分数的模型 $s_{\theta^*}(x, t) = \nabla_x \log p_t(x)$, 我们可以使用基于分数的 MCMC 方法, 例如 Langevin MCMC 或者 HMC 来直接从 $p_t$ 中采样, 并且修正一个数值 SDE solver 的解。
具体来说,在每个时间步骤中,数值 SDE sovler 首先在下一步给出对样本的估计,起着 “predictor” 的作用。然后,基于分数的 MCMC 方法纠正了估计样本的边缘分布,起到了 “corrector” 的作用。这个想法类似于 Predictor-Corrector 方法,这是一个解方程组的数值连续技术家族(Allgower和Georg,2012年),作者同样将其混合采样算法命名为 Predictor-Corrector(PC)采样器。PC采样器泛化了 SMLD和 DDPM 的原始采样方法:前者使用恒等式作为 predictor,annealed Langevin dynamics 作为 corrector,而后者使用 ancestral sampling 作为 predictor 和恒等式作为 corrector。
作者在 SMLD 和 DDPM 模型上测试 PC 采样器(见附录G中的算法2和3),使用 Eq. (1) 和 (3) 给出的原始离散目标进行训练。这展示了 PC 采样器与使用固定数量的噪声尺度训练的基于分数的模型的兼容性。在表1中总结了不同采样器的性能,其中概率流是第4.3节中讨论的 predictor。我们观察到,反向扩散采样器的性能总是优于 ancestral sampling,corrector-only 的方法(C2000)在相同计算下的表现比其他竞争对手(P2000、PC1000)差(事实上,每个噪声尺度需要更多的校正步骤,从而需要更多的计算,以匹配其他采样器的性能)。对于所有 predictors,为每个 predictors 步骤添加一个 corrector 步骤(PC1000)使计算翻倍,但始终提高样本质量(相对P1000)。此外,这通常比在不添加 corrector(P2000)的情况下将 predictor 步数翻一番要好,在P2000中,我们必须为 SMLD/DDPM 模型插值噪声尺度。在图9中,作者提供在 $256 \times 256$ 的 LSUN 图像上用连续目标方程 Eq. (7) 训练的模型 和 VE SDE 的定性比较, 在使用适当数量的 corrector 步骤时,PC采样器在可比计算下明显超过 predictor-only 的采样器。
Probability Flow and Connection to Neural ODEs
基于分数的模型为解决反向时间 SDE 提供了另一种数值方法。对于所有扩散过程,都存在一个相应的确定性过程,其轨迹具有相同的边缘概率密度 ${p_t(x)}_{t=0}^T$ 作为 SDE。 这个确定性过程满足一个 ODE:
\[dx = [f(x, t) - \frac{1}{2} g(t)^2 \nabla_x \log p_t(x)]dt \tag{13}\]一旦分数已知, 那么其由 SDE 确定。 我们叫 Eq. (13) 中的 ODE 叫做 probability flow ODE。 当分数函数由时间依赖的基于分数的模型近似时,该模型通常是神经网络,这是一个 neural ODE的例子。
Exact likelihood computation 利用与 Neural ODEs 的联系,我们可以通过变量公式的瞬时变化计算Eq. (13) 定义的密度。 这使我们能够计算任何输入数据的精确似然。例如,我们在表2的 CIFAR-10 数据集中报告了以 bits/dim 为单位测量的负对数似然(NLL)。
Manipulating latent representations 通过集成 Eq. (13), 我们可以编码任意数据点 $x(0)$ 到一个隐空间 $x(T)$。 解码可以通过为反向时间 SDE 集成相应的 ODE 来实现。就像 neural ODE 和 normalizing flows 等其他可逆模型一样, 我们可以操纵这种隐表征进行图像编辑,例如插值和 temperature scaling (见图3)。
 Uniquely identifiable encoding 与大多数当前的可逆模型不同,我们的编码是唯一可识别的,这意味着在足够的训练数据、模型容量和优化精度下,输入的编码由数据分布唯一确定。 这是因为给定完美的分数估计, 前向 SDE Eq. (5) 没有可训练的参数, 它对应的概率流 ODE Eq.(13) 提供相同的轨迹。
Uniquely identifiable encoding 与大多数当前的可逆模型不同,我们的编码是唯一可识别的,这意味着在足够的训练数据、模型容量和优化精度下,输入的编码由数据分布唯一确定。 这是因为给定完美的分数估计, 前向 SDE Eq. (5) 没有可训练的参数, 它对应的概率流 ODE Eq.(13) 提供相同的轨迹。
Efficient sampling 与 neural ODE 相同, 我们从不同的最终条件 $x(T) \thicksim p_T$ 求解 Eq. (13) 来采样 $x(0) \thicksim p_0$。 使用固定离散化策略,我们可以生成有竞争力的样本,特别是当与 corrector 结合使用时。 使用黑盒ODE求解器不仅可以产生高质量的样本,还可以让我们明确地权衡准确性以获得效率。通过更大的误差容忍度,函数评估的数量可以减少90%以上,而不会影响样本的视觉质量。
Architecture Improvements
作者使用 VE 和 VP SDE 为基于分数的模型探索了几种新的架构设计,其摸模型有与 SMLD/DDPM 相同的离散目标。由于其相似性,我们直接将 VP SDE 的架构迁移到 Sub-VP SDE。VE SDE 的最佳架构名为NCSN++ ,使用PC采样器在CIFAR-10上实现了2.45的FID,而 VP SDE 的最佳架构,称为DDPM++ ,达到2.78。
通过切换 Eq. (7) 中的连续训练目标, 增加网络的深度, 可以进一步提升采样质量。最终的架构叫做 NCSN++ 和 DDPM++ 。表3中报告的结果适用于训练过程中FID最小的 checkpoint,该 checkpoint 使用 PC 采样器生成样本。 相比之下,表2中报告了最后一个训练 checkpoint 的FID分数和NLL值,并使用黑盒 ODE 求解器获得样本。如表3所示,VE SDE 通常比 VP/sub-VP SDE 提供更好的样本质量,但实验中观察到,它们的似然比 VP/sub-VP SDE 更糟。这表明用户可能需要为不同的领域和架构尝试不同的SDE。
我们最好的样本质量模型 NCSN++ cont(deep, VE),将网络深度翻了一番,并为 CIFAR-10 无条件生成的 inception 分数 和 FID 创造了新记录。令人惊讶的是,我们可以实现比之前最好的条件生成模型更好的FID,而无需标记数据。随着所有改进,作者还从基于分数的模型中获得了CelebA-HQ 1024上的高保真采样。最好的似然模型DDPM++ cont.(deep,sub-VP),同样将网络深度翻了一番,并实现了2.99 bit/dim 的对数似然,以 Eq. (7) 的连续目标。
Controllable Generation
框架的连续结构使我们不仅能够从 $p_0$ 中产生数据样本, 如果 $p_t(y \mid x(t))$ 一致, 还可以从 $p_0(x(0) \mid y)$ 中产生数据样本。给定 Eq. (5) 中的前向 SDE, 我们可以从 $p_T(x(T) \mid y)$ 开始从 $p(x(t) \mid y)$ 中采样, 然后求解一个条件反向时间 SDE:
\[dx = \{f(x, t) - g(t)^2 [\nabla_x \log p_t(x) + \nabla_x \log p_t(y \mid x)]\}dt + g(t)d \bar w \tag{14}\]通常, 一旦给定前向过程梯度的估计 $\nabla_x \log p_t(y \mid x(t))$, 我们使用基于分数的生成模型以 Eq.(14) 求解逆问题。 在一些情况下, 可以单独训练一个模型学习前向过程 $\log p_t(y \mid x(t))$ 并且计算它的梯度。或者,我们可以用启发式和领域知识来估计梯度。
我们用这种方法考虑了可控生成的三种应用:class-conditional generation、image imputation 和 colorization。当 $y$ 表示类别标签, 我们训练一个时间依赖的分类器 $p_t(y \mid x(t))$ 作为类条件采样。 由于前向 SDE 是可追溯的, 我们可以轻松地为时间依赖的分类器通过首先从数据集中采样 $(x(0), y)$ 创建训练数据 $(x(t), y)$, 然后采样 $x(t) \thicksim p_{0t}(x(t) \mid x(0))$。 之后,我们可能会在不同的时间步骤中使用交叉熵损失, 像 Eq. (7), 来训练时间依赖的分类器 $p_t(y \mid x(t))$。
Imputation 是条件采样的特殊情况。假设我们有一个不完整的数据点 $y$,其仅仅是一些子集, $\Omega(y)$ 是已知的。 Imputation 负责从 $P(x(0) \mid \Omega(y))$ 中采样, 我们可以用一个无条件模型完成。 Colorization 是 Imputation 的特殊情况,除了已知的数据维度是相同的。我们可以将这些数据维度与正交线性变换解耦,并在变换空间中执行 imputation。 图4(右)显示了使用无条件的基于时间的分数模型实现的 inpainting 和 colorization 的结果。

Appendix
所提出的框架允许具有 matrix-valued 扩散系数的一般 SDE,该系数取决于状态,我们在附录A中对此进行了详细讨论。我们在附录B中给出了 VE、VP 和 sub-VP SDE 的完整推导,并在附录C中讨论如何从从业者的角度使用它们。我们详细阐述了附录D中框架的概率流表述,包括概率流ODE的推导(附录D.1)、精确似然计算(附录D.2)、具有固定离散化策略的概率流采样(附录D.3)、黑盒ODE求解器采样(附录D.4)和唯一可识别编码的实验验证(附录D.5)。我们在附录E给出了中反向扩散采样器、附录F中SMLD模型的DDPM型祖先采样器和附录G中的预测器校正器采样器的完整描述。我们在附录H中解释了我们的模型架构和详细的实验设置,用 $1024 \times 1024$ 的 CelebA-HQ 样本。
The Fraamework for More General SDEs
在正文中,我们介绍了基于简化的SDE Eq. (5) 的框架,其中扩散系数独立于 $x(t)$。 事实证明,所提出的框架可以扩展到更一般的扩散系数。我们可以以如下形式考虑 SDEs:
\(dx = f(x, t)dt + G(x, t)dw \tag{15}\) 其中 $f(·, t): R^d \rightarrow R^d$ 和 $G(·, t): R^d \rightarrow R^{d \times d}$。 接下来解释贯穿全文的 SDEs。
反向时间 SDE 由下式给定:
\(dx = \{f(x, t) - \nabla · [G(x, t)G(x, t)^\top] - G(x, t)G(x, t)^\top \nabla_x \log p_t(x)\}dt + G(x, t)d\bar w \tag{16}\) 其中,我们定义 $\nabla · F(x) := (\nabla · f^1(x), \nabla · f^2(x), …, \nabla f^d(x))^\top$ 对于 matrix-valued 函数 $F(x):= (f^1(x), f^2(x), …, f^d(x))$ 贯穿全文。
对应于 Eq. (15) 的概率流 ODE 有如下形式, 推导见附录 D.1:
\[dx = \{f(x, t) - \frac{1}{2} \nabla · [G(x, t) G(x, t)^\top ] - \frac{1}{2} G(x, t) G(x, t)^\top \nabla_x \log p_t(x)\}dt \tag{17}\]最终对于通用 SDE Eq. (15) 的条件生成, 我们可以求解如下的条件反向时间 SDE, 细节在附录 I:
\(dx = \{f(x, t) - \nabla · [G(x, t)G(x, t)^\top] - G(x, t)G(x, t)^\top \nabla_x \log p_t(x) - G(x, t)G(x, t)^\top \nabla_x \log p_t(y \mid x)\}dt + G(x, t)d \bar w \tag{18}\) 当一个 SDE 的 drift 和 diffusion 系数不相似的时候,以闭式解的形式计算 transition kernel $p_{0t}(x(t) \mid x(0))$ 非常困难。这阻碍了基于分数的模型的训练, 因为 Eq. (7) 需要知道 $\nabla_{x(t)} \log p_{0t}(x(t) \mid x(0))$。 例如, 当使用 sliced score matching 时, Eq. (7) 的训练目标变成:
\[\theta^* = \arg \min_\theta E_t \{\lambda(t) E_{x(0)} E_{x(t)}E_{v \thicksim p_v}[\frac{1}{2}\|s_\theta(x(t), t)\|_2^2 + v^\top s_\theta(x(t), t)v]\} \tag{19}\]其中 $\lambda: [0, T] \rightarrow R^+$ 是正加权函数, $t \thicksim U(0, T)$, $E[v] = 0$ 并且 $Cov[v] = I$。 我们总是可以仿真 SDE 从 $p_{0t}(x(t) \mid x(0))$ 里采样, 并且求解 Eq. (19) 来训练时间依赖的基于分数的模型 $s_\theta(x, t)$。
VE, VP and Sub-VP SDEs
下面我们提供了详细的推导,以证明 SMLD 和 DDPM 的噪声扰动分别是 Variance Exploding(VE) 和Variance Preserving(VP) SDEs 的离散化。我们还引入了 Sub-VP SDE,这是对 VP SDE的修改,通常在样品质量和似然方面实现更好的性能。
首先, 当使用总共 N 个噪声尺度, 每个 SMLD 的扰动核 $p_{\sigma_i}(x \mid x_0)$ 可以通过下面的马尔科夫链推导得到:
\(x_i = x_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2} z_{i-1}, \quad i = 1, ..., N \tag{20}\) 其中 $z_{i-1} \thicksim N(0, I)$, $x_0 \thicksim p_{data}$ , 并且我们引入 $\sigma_0 = 0$ 简化表示。 在 $N \rightarrow \infty$ 的限制下, 马尔科夫链 ${x_i}{i=1}^N$ 变成一个连续随机过程 ${x(t)}{t=0}^1$, ${\sigma_i}_{i=1}^N$ 变成一个函数 $\sigma(t)$, $z_i$ 变成 $z(t)$, 其中我们有一个用于索引的连续时间变量 $t \in [0, 1]$, 而不是一个整数 $i \in {1, 2, …, N}$。 对于 $i = 1, 2, …, N$, 令 $x(\frac{i}{N}) = x_i$, $\sigma(\frac{i}{N}) = \sigma_i$ 和 $z(\frac{i}{N}) = z_i$。 我们用 $\Delta t = \frac{1}{N}$ 和 $t \in {0, \frac{1}{N}, …, \frac{N-1}{N}}$ 重写 Eq. (20):
\[x(t + \Delta t) = x(t) + \sqrt{\sigma^2(t + \Delta t) - \sigma^2(t)} z(t) \approx x(t) + \sqrt{\frac{d[\sigma^2(t)]}{dt} \Delta t} z(t)\]当 $\Delta t \ll 1$ 时, 约等于成立。 在 $\Delta t \rightarrow 0$ 的限制下, 收敛为:
\[dx = \sqrt{\frac{d[\sigma^2(t)]}{dt}}dw \tag{21}\]这便是 VE SDE。
对于 DDPM 中是用的扰动核 ${p_{\alpha_i}(x \mid x_0)}_{i=1}^N$, 离散马尔科夫链为:
\[x_i = \sqrt{1- \beta_i} x_{i-1} + \sqrt{\beta_i} z_{i-1}, \quad i=1, ..., N \tag{22}\]其中 $z_{i-1} \thicksim N(0, I)$。 当 $N \rightarrow \infty$ , 为了得到马尔科夫链的限制, 我们定义一个辅助噪声尺度集合 ${\bar \beta_i = N \beta_i}_{i=1}^N$, 然后重写 Eq. (22) 如下:
\[x_i = \sqrt{q - \frac{\bar \beta_i}{N}} x_{i-1} + \sqrt{\frac{\bar \beta_i}{N}} z_{i-1}, \quad i = 1, ..., N \tag{23}\]在 $N \rightarrow \infty$ 的限制下, ${\bar \beta_i}_{i=1}^N$ 变成一个由 $t \in [0, 1]$ 索引的函数 $\beta(t)$。 令 $\beta(\frac{i}{N}) = \bar \beta_i, x(\frac{1}{N}) = x_i, z(\frac{i}{N}) = z_i$。 我们可以用 $\Delta t = \frac{1}{N}$ 和 $t \in {0, 1, …, \frac{N-1}{N}}$ 重写 Eq. (23) 的马尔科夫链:
\[\begin{aligned} x(t + \Delta t) &= \sqrt{1 - \beta(t + \Delta t) \Delta t} x(t) + \sqrt{\beta(t + \Delta t) \Delta t} z(t) \\ &\approx x(t) - \frac{1}{2} \beta(t + \Delta t) \Delta t x(t) + \sqrt{\beta(t + \Delta t)\Delta t} z(t) \\ &\approx x(t) - \frac{1}{2}\beta(t)\Delta t x(t) + \sqrt{\beta(t)\Delta t} z(t) \end{aligned} \tag{24}\]当 $\Delta t \ll 1$ 时, 约等于成立。 因此, 在 $\Delta t \rightarrow 0$ 的限制下, Eq. (24) 收敛到如下的 VP SDE:
\[dx = -\frac{1}{2} \beta(t) x dt + \sqrt{\beta(t)} dw \tag{25}\]到目前为止,我们已经证明,SMLD 和 DDPM 中使用的噪声扰动分别对应于 VE 和 VP SDE 的离散化。当 $t \rightarrow \infty$ 时, VE SDE 总是产生方差爆炸的过程。 而 VP SDE 产生方差有界的过程。此外, 当 $p(x(0))$ 为单位方差, 那么该过程对所有 $t \in [0, \infty)$ 有常数单位方差。因为 VP SDE 有相似的 drift 和 diffusion 系数, 我们使用 Sa ̈rkka ̈ & Solin (2019) 中的 Eq. (5.51) 来得到一个 ODE, 其主导方差的变化:
\[\frac{d \Sigma_{VP}(t)}{dt} = \beta(t)(I - \Sigma_{VP}(t))\]其中 $\Sigma_{VP}(t) := Cov[x(t)] \quad \text{for } {x(t)}_{t=0}^1$ 服从一个 VP SDE。 求解这个 ODE, 我们得到:
\[\Sigma_{VP}(t) = I + e^{\int_0^t -\beta(s)ds} (\Sigma_{VP}(0) - I) \tag{26}\]从这里我们可以看到方差 $\Sigma_{VP}(t)$ 总是以 $\Sigma_{VP}(0)$ 为界。此外, $\Sigma_{VP}(t) \equiv I \quad \text{if } \Sigma_{VP}(0) = I$。 由于这种差异, 我们吧 Eq. (9) 叫做 Variance Exploding (VE) SDE, 并且把 Eq. (11) 叫做 Variance Preserving (VP) SDE。
受 VP SDE 的启发,作者提出了一个新的SDE,称为 Sub-VP SDE,即:
\[dx = -\frac{1}{2} \beta(t)x dt + \sqrt{\beta(t)(1 - e^{-2 \int_0^t \beta(s)ds})} dw \tag{27}\]遵循标准的推导, 很直觉地发现 $E[x(t)]$ 对于 VP 和 Sub-VP SDEs 都是相同的; sub-VP SDEs 的方差函数不同:
\[\Sigma_{sub-VP}(t) = I + e^{-2\int_0^t \beta(s)ds}I + e^{-\int_0^t \beta(s)ds}(\Sigma_{sub-VP}(0) - 2I) \tag{28}\]对于过程 ${x(t)}{t=0}^1$ 的 $\Sigma{sub-VP}(t) := Cov[x(t)]$ 通过求解 Eq. (27) 得到。此外,作者观察到: (i) 对所有 $t \geq 0$ , $\Sigma_{sub-VP}(0) = \Sigma_{VP}(0)$ 并且共享 $\beta(s)$, 有 $\Sigma_{sub-VP}(t) \preccurlyeq \Sigma_{VP}(t)$; 并且 (ii) 如果 $\text{lim}{t \rightarrow \infty} \int_0^t \beta(s)ds = \infty$, 有 $\text{lim}{t \rightarrow \infty} \Sigma_{sub-VP}(t) = \text{lim}{t \rightarrow \infty} \Sigma{VP}(t) = I$ 。
Controllable Generation
Imputation
Imputation 是条件采样的一个特殊情况。将 $\Omega(x)$ 和 $\bar \Omega(x)$ 分别表示为 $x$ 的已知和未知维度, 令 $f_{\bar \Omega}(·,t)$ 和 $G_{\bar \Omega}(·, t)$ 表示服从未知维度的 $f(·, t)$ 和 $G(·, t)$。 对于 VE/VP SDEs, drift 系数 $f(·, t)$ 是 element-wise 的, diffusion 系数 $G(·, t)$ 是对角的。当 $f(·, t)$ 是 element-wise 的, $f_{\bar \Omega}(·, t)$ 表示应用于未知维度的 element-wise 函数。当 $G(·, t)$ 是对角的,$G_{\bar \Omega(·, t)}$ 表示服从于未知维度的子矩阵。
对于 imputation, 我们的目标是从 $p(\bar \Omega(x(0)) \mid \Omega(x(0)) = y)$。 定义一个新的扩散过程 $z(t) = \bar \Omega(x(t))$, 对 $z(t)$ 的 SDE 可以写作:
\[dz = f_{\bar \Omega}(z, t) dt + G_{\bar \Omega}(z, t) dw\]以 $\Omega(x(0)) = y$ 为条件, 反向时间 SDE 为:
\[dz = \{f_{\bar \Omega(z, t)} - \nabla · [G_{\bar \Omega}(z, t) G_{\bar \Omega}(z, t)^\top] - G_{\bar \Omega}(z, t)G_{\bar \Omega}(z, t)^\top \nabla_z \log p_t(z \mid \Omega(z(0)) = y)\}dt + G_{\bar \Omega}(z, t) d\bar w\]尽管 $p_t(z(t) \mid \Omega(x(0)) = y)$ 通常无法得到, 但是它可以被估计。 用 $A$ 表示 $\Omega(x(0)) = y$, 有:
\[\begin{aligned} p_t(z(t) \mid \Omega(x(0)) = y) = p_t(z(t) \mid A) &= \int p_t(z(t) \mid \Omega(x(t)), A) p_t(\Omega(x(t)) \mid A) d \Omega(x(t)) \\ &= E_{p_t(\Omega(x(t)) \mid A)}[p_t(z(t) \mid \Omega(x(t)), A)] \\ &\approx E_{p_t(\Omega(x(t) \mid A)}[p_t(z(t) \mid \Omega(x(t)))] \\ &\approx p_t(z(t) \mid \hat \Omega(x(t))) \end{aligned}\]其中 $\hat \Omega(x(t))$ 是从 $p_t(\Omega(x(t)) \mid A)$ 随机采样,这是一个 tractable 的分布。 因此:
\[\begin{aligned} \nabla_z \log p_t(z(t) \mid \Omega(x(0)) = y) &\approx \nabla_z \log p_t(z(t) \mid \hat \Omega(x(t))) \\ &= \nabla_z \log p_t([z(t); \hat \Omega(x(t))]) \end{aligned}\]其中 $[z(t); \hat \Omega(x(t))]$ 表示一个向量 $u(t)$, 使得 $\Omega(u(t)) = \hat \Omega(x(t))$ 并且 $\bar \Omega(u(t)) = z(t)$ , 保持恒等因为: $\nabla_z \log p_t ([z(t); \hat \Omega(x(t))]) = \nabla_z \log p_t(z(t) \mid \hat \Omega(x(t))) = \nabla_z \log p_t(z(t) \mid \hat \Omega(x(t)))$。
-
Previous
【深度学习】VoxelNet:End-to-End Learning for Point Cloud Based 3D Object Detection -
Next
【深度学习】SECOND: Sparsely Embedded Convolutional Detection